Animal Science and Technology & Applied Statistics

3 minute read

RNN & Seq2Seq

Transformer를 알기 전, RNN부터 알아야한다.

“RNN은 연속적인(시계열) 데이터에 잘 동작하는 네트워크 구조이다.”“

CNN은 이미지 구역별로 같은 weight를 공유한다면,

RNN은 시간 별로 같은 weight를 공유한다.

즉, 과거와 현재는 같은 weight를 공유한다.

First Order system : 현재 시간의 상태가 이전 시간의 상태와 관련이 있다고 가정

  • 입력이 없는 경우
    • $x_t = f(x_{t-1}))$
    • $x_t$ : $t$일때 상태
    • 이 시스템은 외부 입력 없이 자기 혼자서 돌아간다.
  • 입력이 있는 경우 현재 시간의 상태($x_t$)가 이전 시간의 상태($x_t$)와 현재 입력($u_t$)에 관계 있는 경우
    • $x_t = f(x_{t-1},u_t)$
  • 모든 $x_t$가 관측이 가능한가?
    • $x_t$의 일부만 관찰이 가능한 경우가 많다.
    • 각 시간에서 관측 가능한 상태의 모음 : 출력 $y_t$라고 하자.
    • $y_t = h(x_t), x_t = f(x_{t-1},u_t)$
    • 입력 $u_t$ , 출력 $y_t$의 형태가 존재하는 Neural Network가 형성

  • 어떤 시스템을 해석하기 위한 3요소 : 입력, 상태, 출력

  • 이를 그림으로 표현하면

    image-20240630040415289

    RNN과 ANN의 대표적인 차이는 self-feed back의 유무이다.

    시간에 따른 자세하게 표현하면 아래와 같다.

    image-20240630040736444

  • 여기서 상태 $x_t$가 의미하는 것은 : hidden layer state

  • 앞의 그림에서 상태 $x_t$는 이전까지의 상태와, 이전까지의 입력을 대표할 수 있는 압축본이라고 할 수 있다.

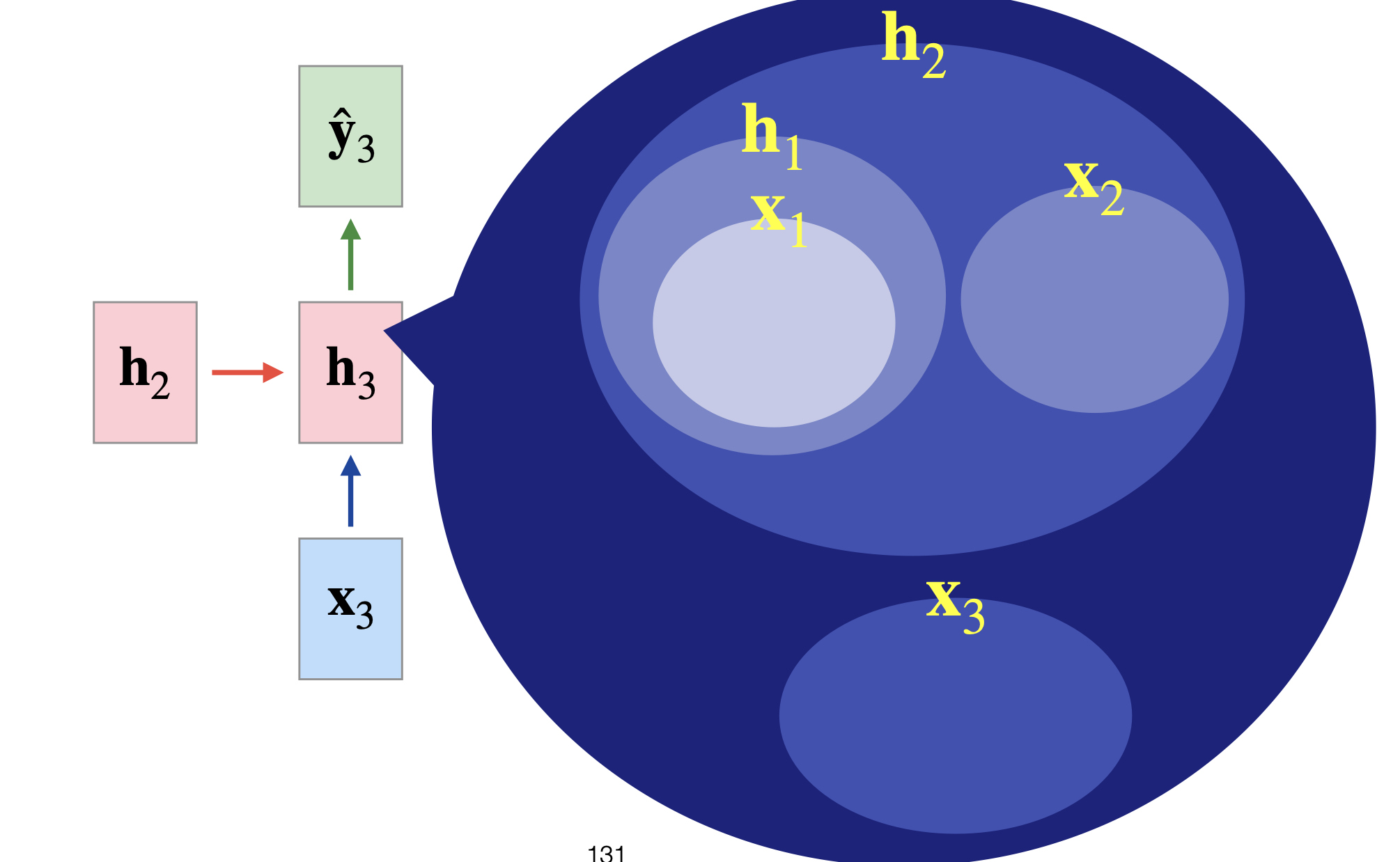
image-20240628181909067

  • 여기서 $W_x, W_h, W_y, b, b_y$는 시간에 따라 다르지 않다.
  • 상태 $x_t$는 시계열로 들어오는 입력들을 최대한 상세히 표현할 수 있어야한다.

원래 풀고 싶었던 문제 : $x_t = f(u_t, u_{t-1}, u_{t-2}, … , u_0)$

대신 해서 풀 문제 : $x_t = f(x_{t-1}, u_t)$

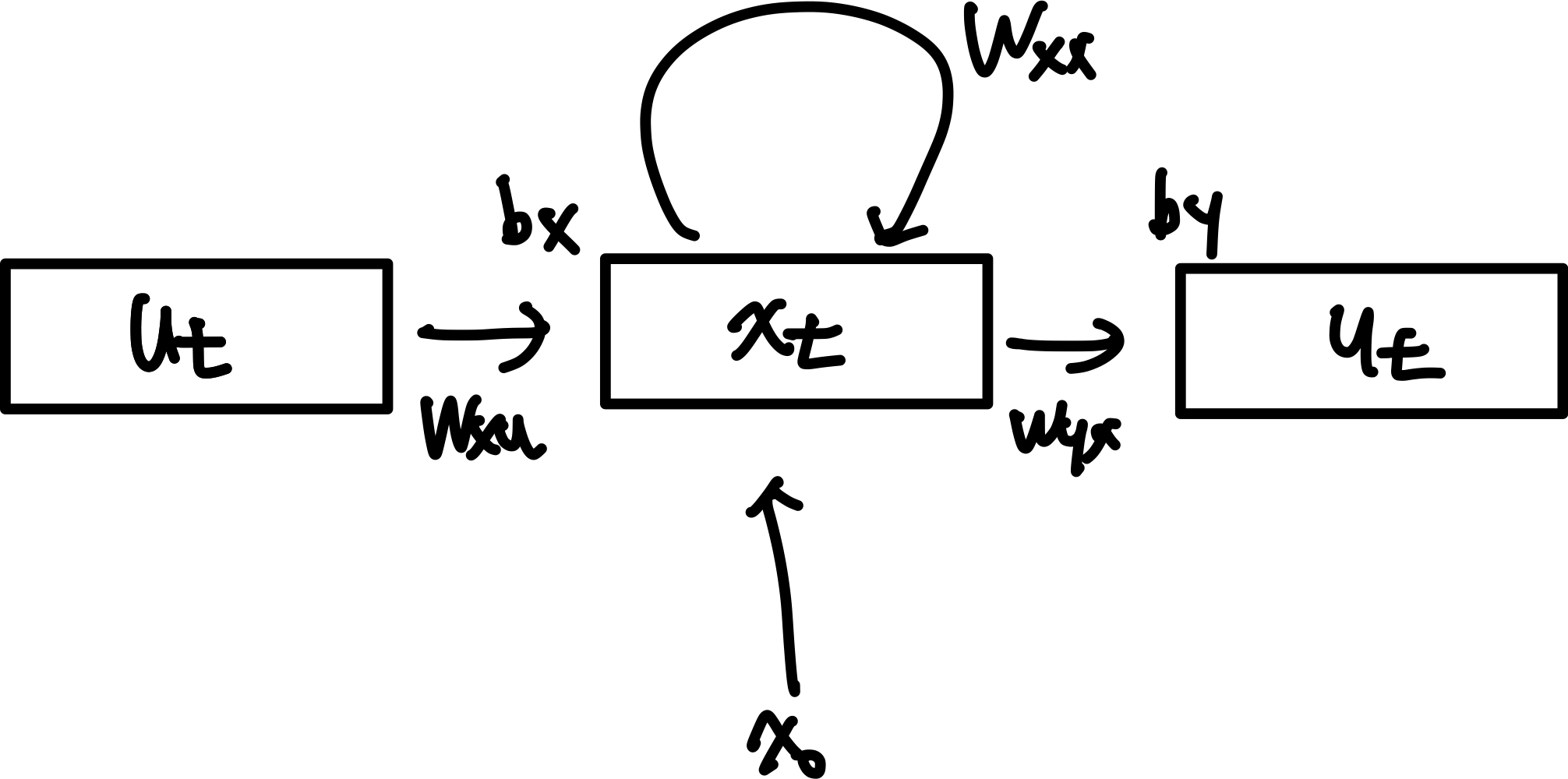
State-Space Model 에서 근사하는 함수는 2개 \(x_t = f(x_{t-1}, u_t)\\ y_t = h(x_t)\) 함수 $f$와 $h$를 근사하기 위해 뉴럴 네트워크를 사용한다.

먼저 뉴럴 네트워크에서 비선형 표현하는 방법은 $y = \sigma(w^Tx + b)$이다.

이 식을 통해 함수 $f$와 $h$를 근사하면 \(x_t = \sigma(W_{xx}x_{t-1} + W_{xu}u_t+b_x) \\ y_t = \sigma(W_{yx}x_t+b_y)\) 사용하는 parameter matrix matrix는 총 5개이다.

이를 다시 간략하게 그림으로 표현하면 아래와 같다.

image-20240630042301484

  • Training할 때는 ANN, CNN 처럼 back-propagation을 이용한다.

  • RNN은 아래와 같은 유형이 있다.

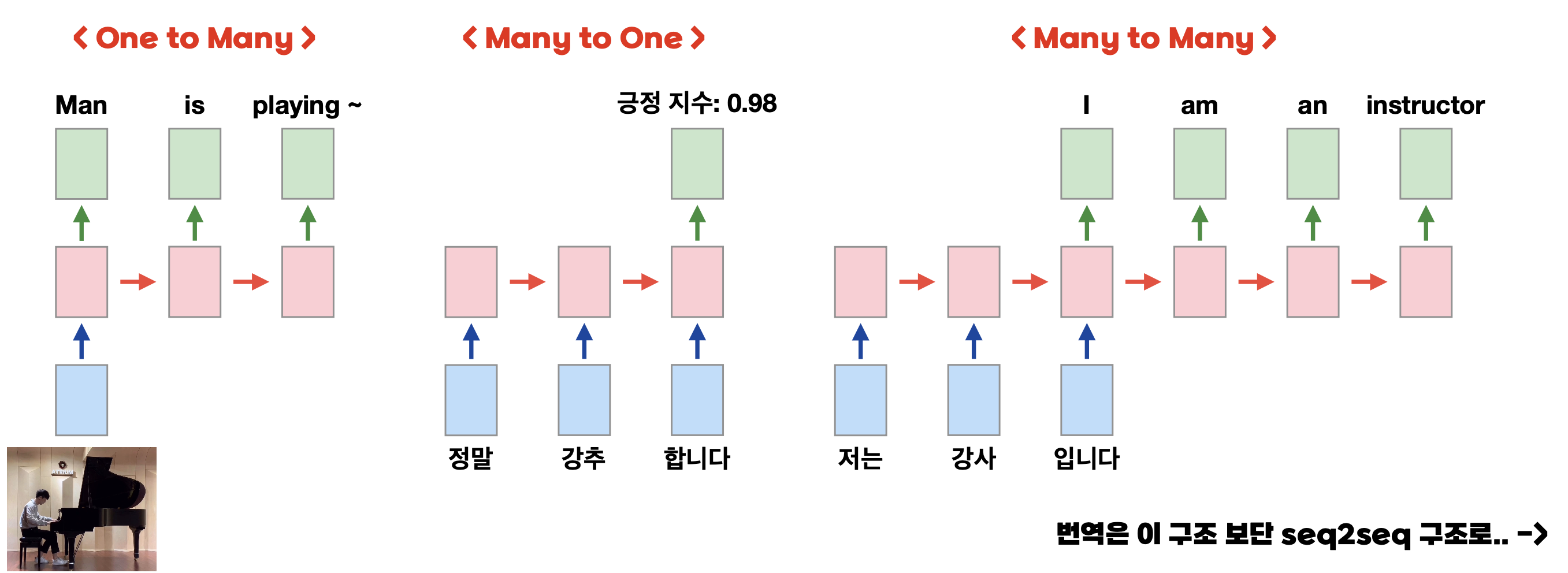
image-20240629233135329

One to Many는 주로 생성할 때,

Many to Many 는 주로 번역할 때 사용되지만 RNN에서는 거의 사용되지 않는다.

-> seq2seq에서 주로 사용된다.(Many to One + One to Many)

이와 같이 $h$(현재 상태) 는 이전의 정보를 가진다.

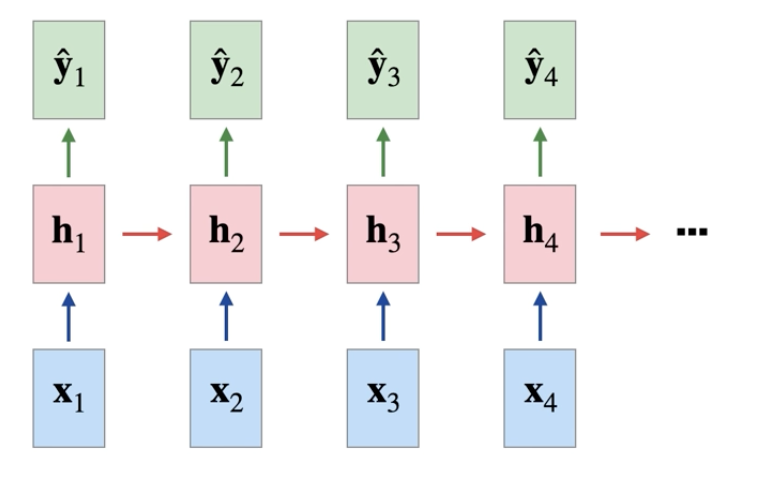
image-20240628182054796

다음에 어떤 알파벳(one-hot encoded)이 나와야 할까? => 다중 분류네!

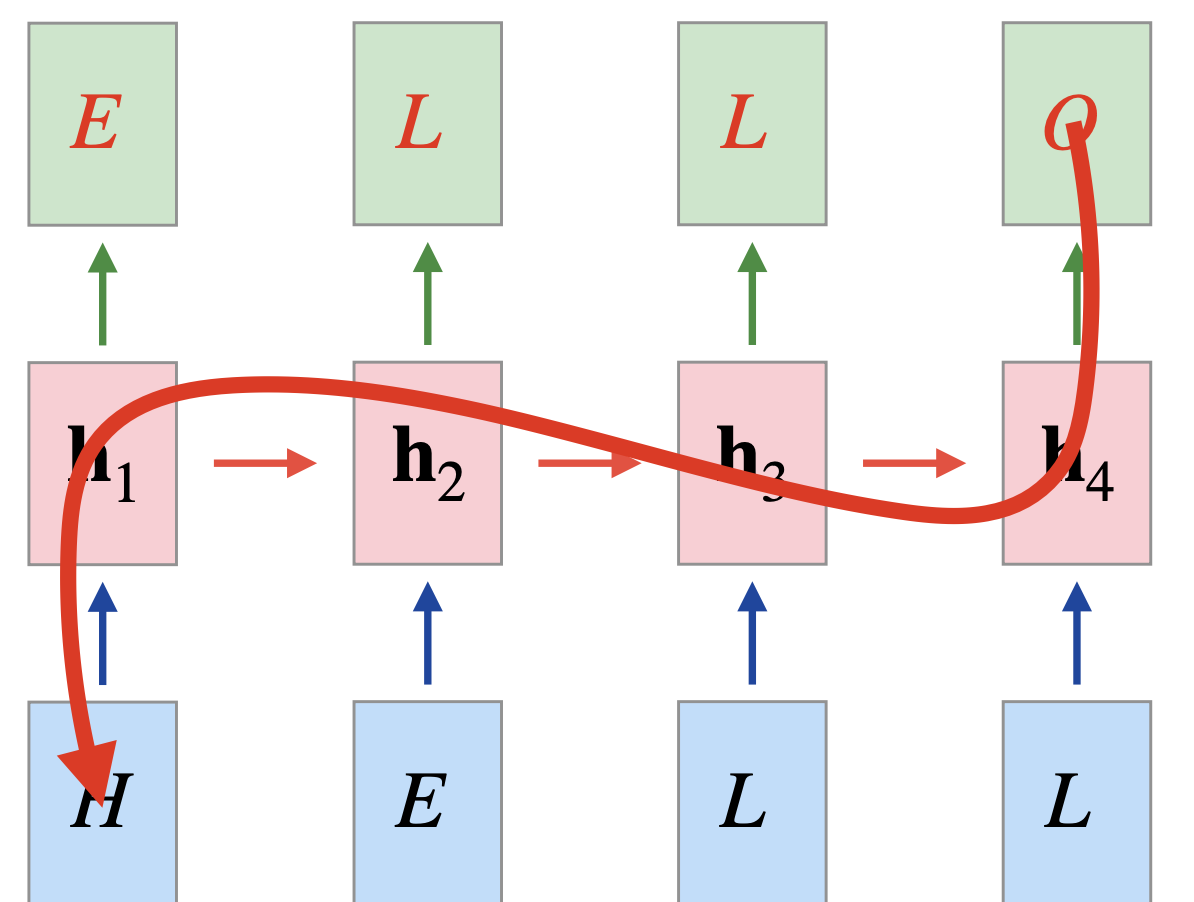
image-20240628183547905

=> ŷ 을 softmax 통과시켜서 cross-entropy 계산 => ELLO 네개 글자에 대해 cross-entropy 더해주면 되겠다

근데 O가 나오게 하기 위해 H가 gradient 에 미치는 영향력?

멀수록 잊혀진다!(back propagation) 또, 갈수록 흐려진다!(forward propagation) <- tanh 때문

이 둘 모두 RNN의 구조적 한계이다.

이 RNN에 Attention을 추가한 것이 seq2seq이다.

seq2seq

  • 각각의 cell은 plain RNN에서 발전된 형태인 LSTM이나 GRU를 주로 사용한다.

  • input으로 sequence를 받는다.(word, image 등등)

  • output으로 다른 sequence를 내놓는다.

  • 위처럼 세개의 item이 들어가도 4개의 item이 출력될 수 있다.

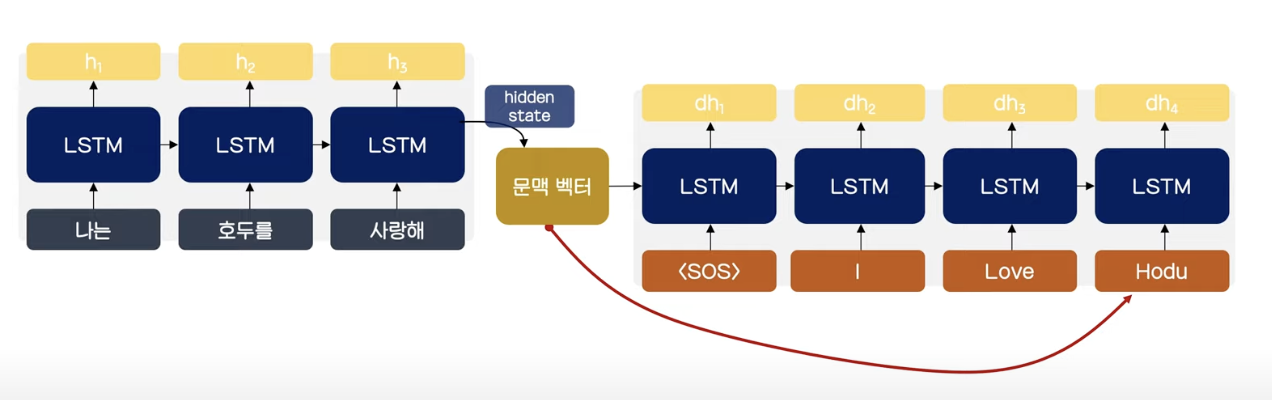
    image-20240630053332916

  • encoder(입력된 정보를 어떻게 저장할 것인가), decoder(압력된 정보를 어떻게 해석할 것인가, 어떻게 출력할 것인가) 두 파트로 구성된다.

  • encoder: 각각의 input sequence를 processes하여, 그것들이 가지고 있는 정보들을 compile하여 하나의 벡터(context vector, 문맥벡터)로 정의한다.

  • decoder : context vector을 받아서 output sequence를 item by item으로 표현한다.

    아래 영상이 이를 잘 보여준다.

이를 펼쳐서 보면 아래와 같다.

seq2seq의 문제점

  • 문맥 벡터가 encoder의 모든 시퀀스의 정보를 포함하고 있기때문에 decoding 시 개별 토큰과의 관계 파악이 어렵다.
  • context vector에 마지막 단어의 정보가 가장 많이 담긴다.
    • 즉 마지막 단어를 가장 열심히 본다.
  • 멀수록 잊혀진다는 문제를 해결하지 못했다 ->Sequence가 길어지는 경우 RNN의 고질적인 문제인 기울기 소실 위험

이를 해결하기 위해 LSTM, GRU를 통해 해결하고자 하였다.

하지만 완벽히 해결할 수 없고, Attention 개념이 등장했다.

Seq2Seq with Attention

어텐션이란 모델이 각각의 input sequence 중에서 output sequence에서 주목해야하는 part를 direct로 가중치를 줘서 정보를 더 잘 활용할 수 있도록 한다.

Attention이 가미된 Seq2Seq는 아래 그림과 같다.

  1. encoder가 더이상 파이널 히든 스테이트 뿐만 아니라, 전체 hidden state를 디코더에 넘겨주기 때문에 보다 많은 정보를 넘겨준다.

  2. decoder가 필요한 hidden state 중 필요한 정보를 취사선택한다.

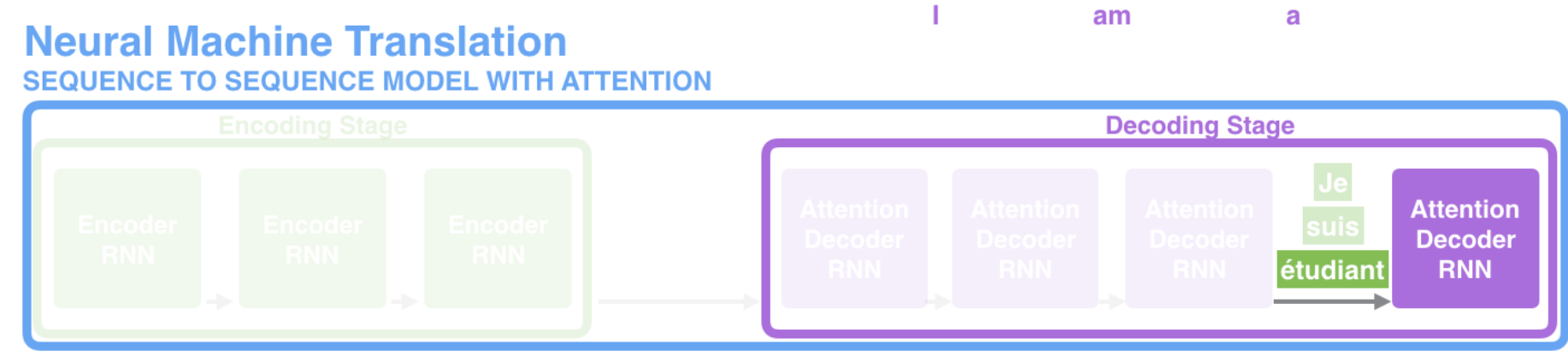
image-20240630060146825

  1. decoder은 encoder가 전달하는 여러개의 hidden state를 extra step을 수행한다.

    extra step : encoder가 보내준 각각의 hidden state는 해당하는 단어의 sequence에 가장 큰 영향을 받을텐데, 이에 대한 score를 부여한다.

    score에 대해 softmax를 수행한 후 모두 결합한다.

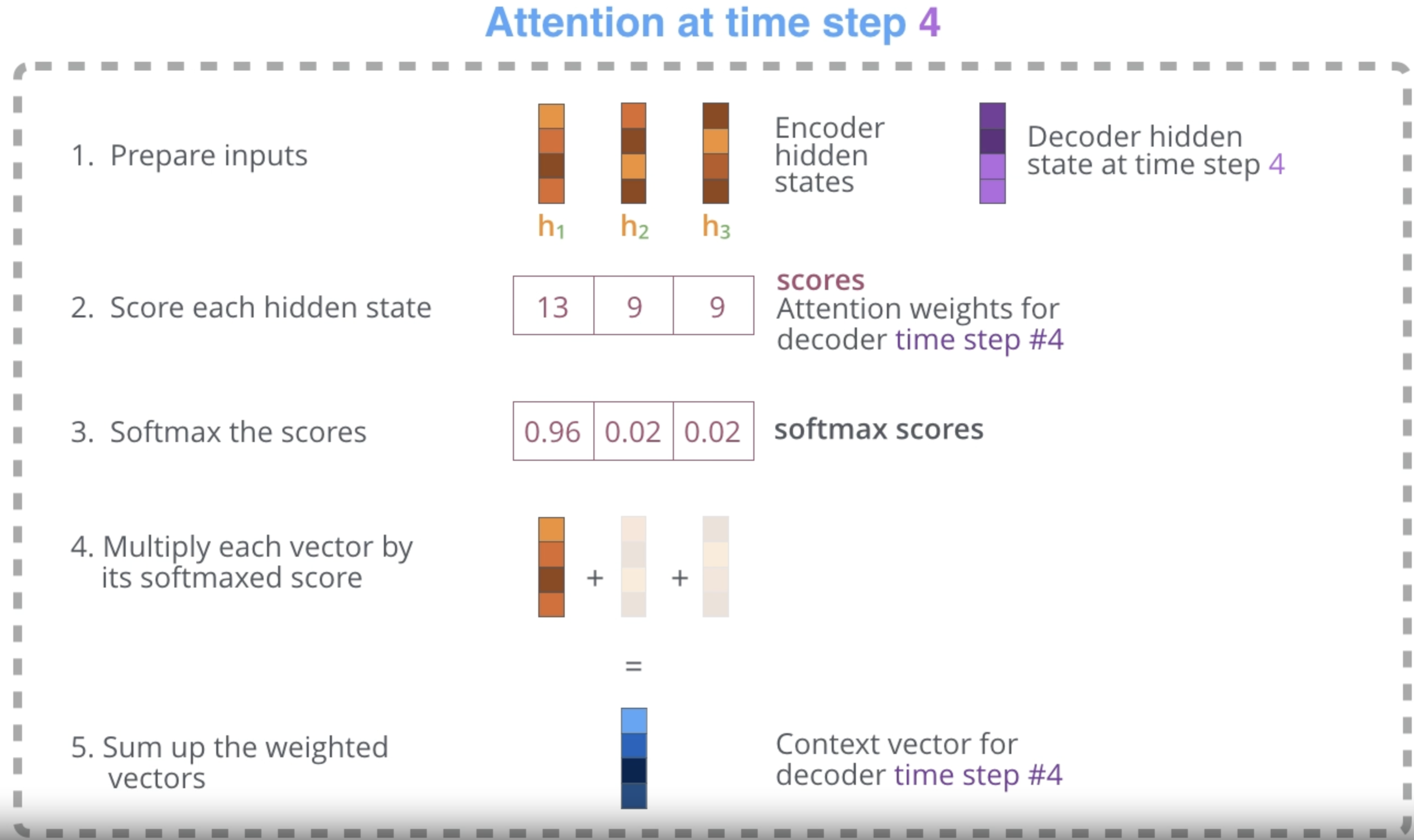
    image-20240630061444358

일반적으로 hidden state vector와 context vector를 concatenate한다.

(따라서 전체 사이즈는 hidden state vector + context vector)

발전 방향 : RNN -> RNN + Attention -> 트랜스포머

  • RNN + Attention의 구조적인 한계 : 흐려지는 정보에 Attention한다.

  • EX ) ‘쓰다’라는 단어의 뜻을 이해할려면 멀리 있는 선행 단어를 봐야 알 수 있는데, 흐려진채로 들어가니 의미를 잘 못 담는 문제 발생 ** **-> bidirection RNN을 써야한다.

  • 트랜스포머는 attention을 적극활용 : self-attention을 통해 RNN (구조)을 완전히 버렸다.
    • Decoder가 마지막 단어만 열심히 보는 문제 (갈수록 흐려진다.) <- attention으로 해결
    • RNN의 vanishing gradient (멀수록 잊혀진다) <- self-attention으로 해결
    • 흐려지는 정보에 attention

다음 포스터에서 트랜스포머에 대해 포스팅하도록 하겠다.

Reference

https://jalammar.github.io/illustrated-transformer/

You may also enjoy

RAG

10 minute read

RAG