[Paper Review] Attention Is All You Need
Attention Is All You Need

You got me looking for attention
…
Attention is what I want
Attention Is All You Need에서 가장 주목해야하는 점은
- 어떻게 ‘RNN’을 사용하지않고 성능과 학습속도를 증가시켰는가?
- Self-Attention이란 무엇인가?
- 포지셔닝 인코딩이란 무엇인가?
이다.
아래는 위 질문에 대한 간략한 설명과, Attention is all you need에서 말하고자 하는 것을 시각화를 통해 요약하였다.
(Jay alamma에게 경의를!)
트랜스포머는 기존 encoder, decoder을 발전시킨 딥러닝 모델이다.
가장 큰 차이점은 RNN을 사용하지않는 점이다.
기존 RNN을 사용하지 않고 학습이 빠르고 성능이 좋기에 큰 관심을 이끌었다.
트랜스포머는 어떻게 더 빠르게 학습이 될 수 있을까에 대한 한마디 답은 병렬화이다.
RNN이 순차적으로 첫번째부터 마지막까지 계산해 인코딩하는 반면 트랜스포머는 한번에 이 과정을 처리한다.
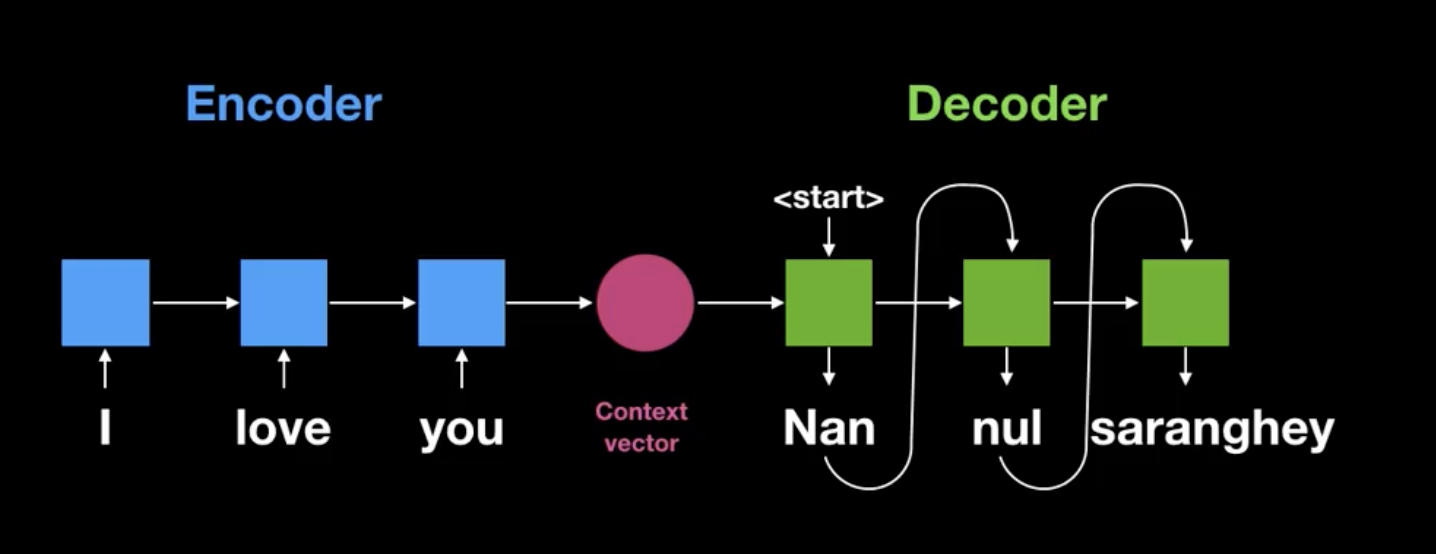
이 과정이 기존 전통적인 Encoder, Decoder 모델이다.
context vector의 크기가 고정이므로 input이 커질수록, 번역이 엉터리가 되는 경우가 많다.
이를 Attention을 통해 진보된 Encoder, Decoder모델이 등장했다.
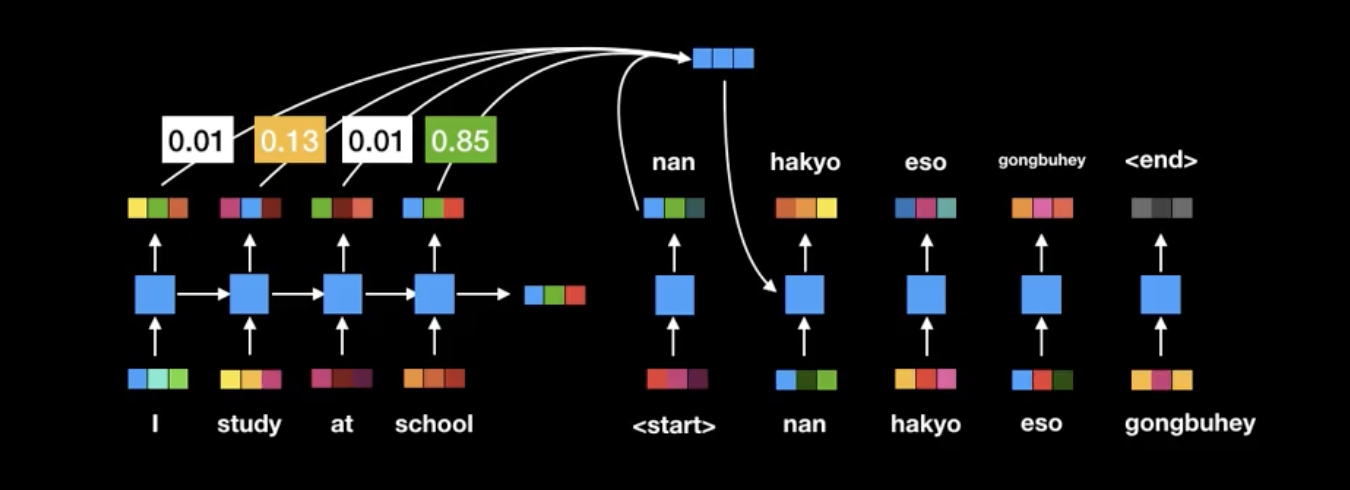
이는 고정된 크기의 context vector를 사용하지않고, 단어를 하나씩 번역할 때마다 어텐션 메커니즘을 통해 효율적인 번역을 하는 장점이 있다.
따라서 긴 문장의 번역 성능이 기존의 모델보다 상당히 성능이 좋아졌다.
하지만 RNN을 순차적으로 계산하여 느리다는 점과, 성능의 한계를 보였다.
이 한계를 극복한 모델이 바로 Transformer이다.
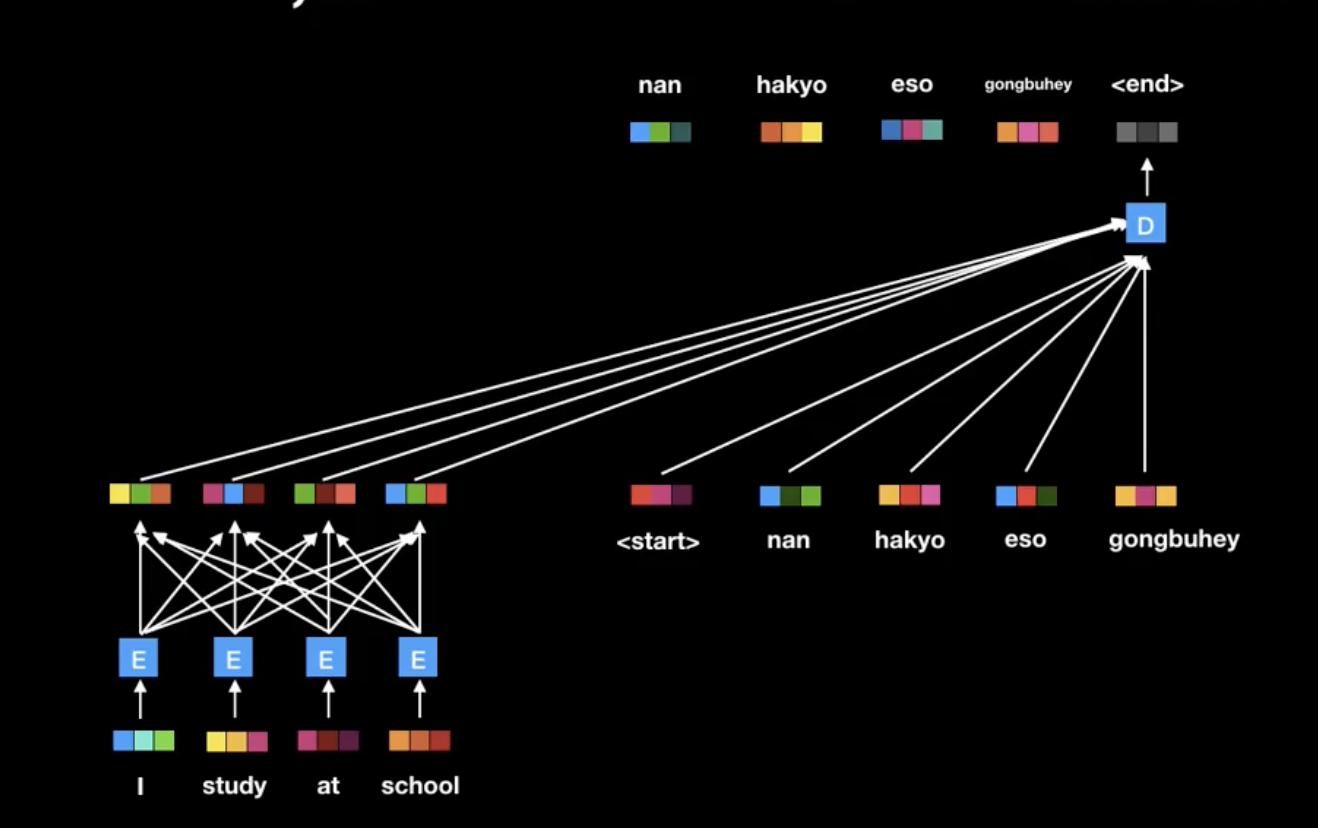
RNN의 순차적인 계산은 트랜스포머의 행렬의 곱으로 해결했다.
또한 Transformer Decoder 연산과정은 어텐션 기반 encoder, decoder과 닮아있다.
트랜스포머의 가장 큰 장점은 RNN을 성공적으로 제거한 점이다.
이를 통해 학습시간을 크게 감축하고 성능을 높였다.
RNN이 없는 트랜스포머는 어떻게 위치 정보를 처리할 수 있을까
바로 포지셔닝 인코딩이다.
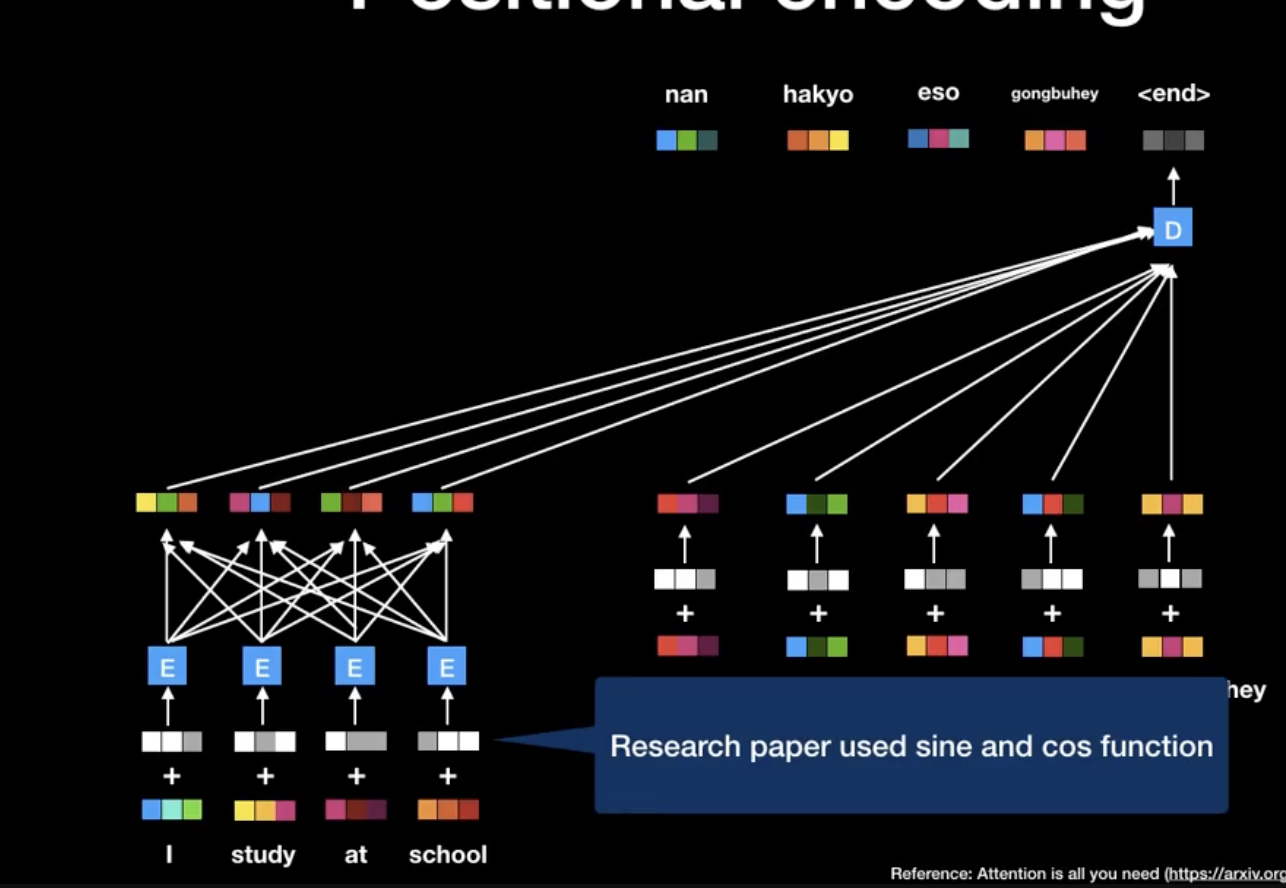
포지셔닝 인코딩은 크게 두가지 장점이 있다.
- 항상 포지셔닝 인코딩은 -1~+1로 할당된다.
- 모든 포지셔닝 인코딩은, 상대적인 인코딩 값을 줄 수 있다.


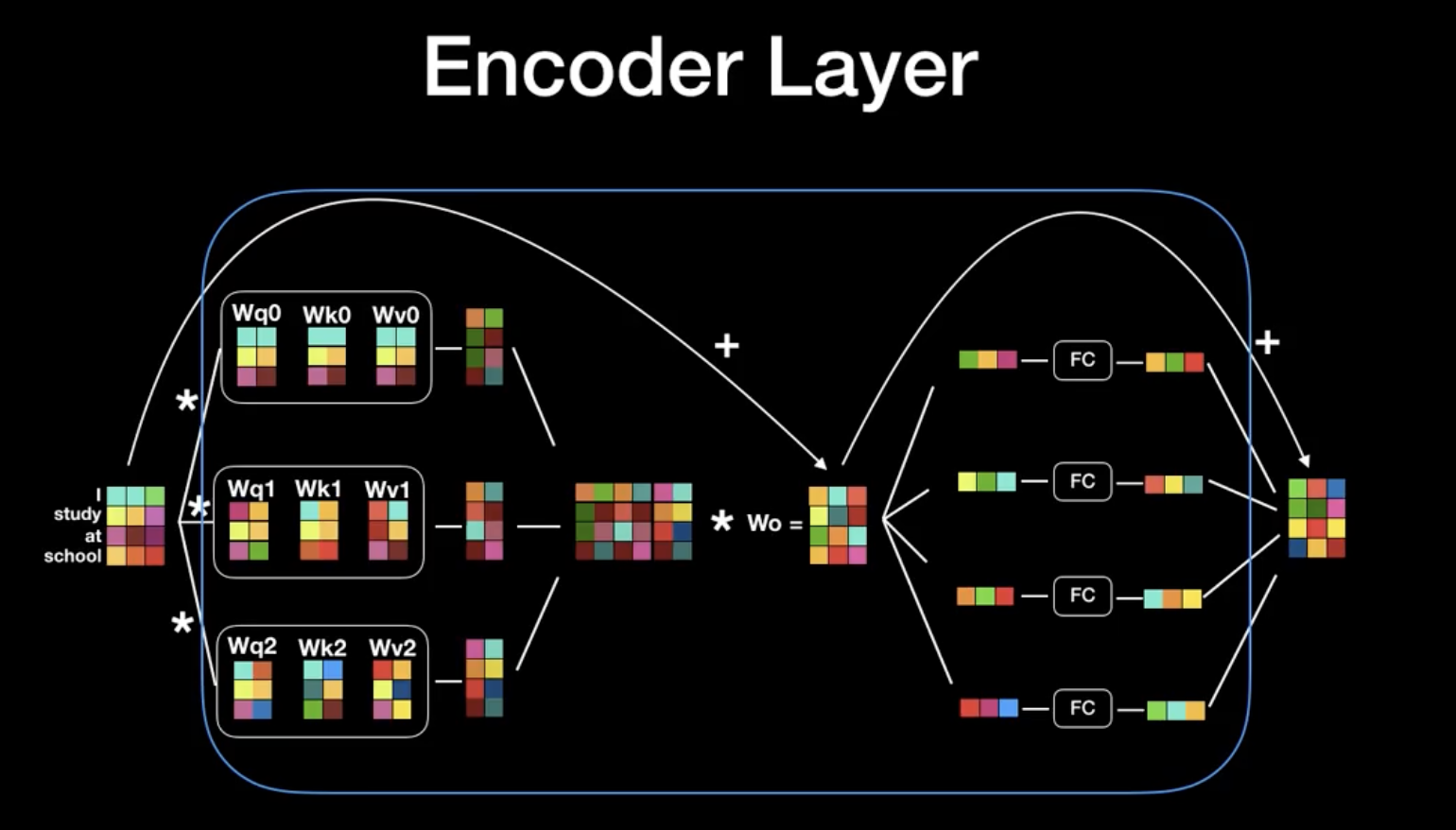
출력벡터의 차원의 크기와 입력벡터의 차원의 크기가 같다.
이는 즉슨, encoder layer를 여러개 붙일 수 있다는 점을 시사한다.
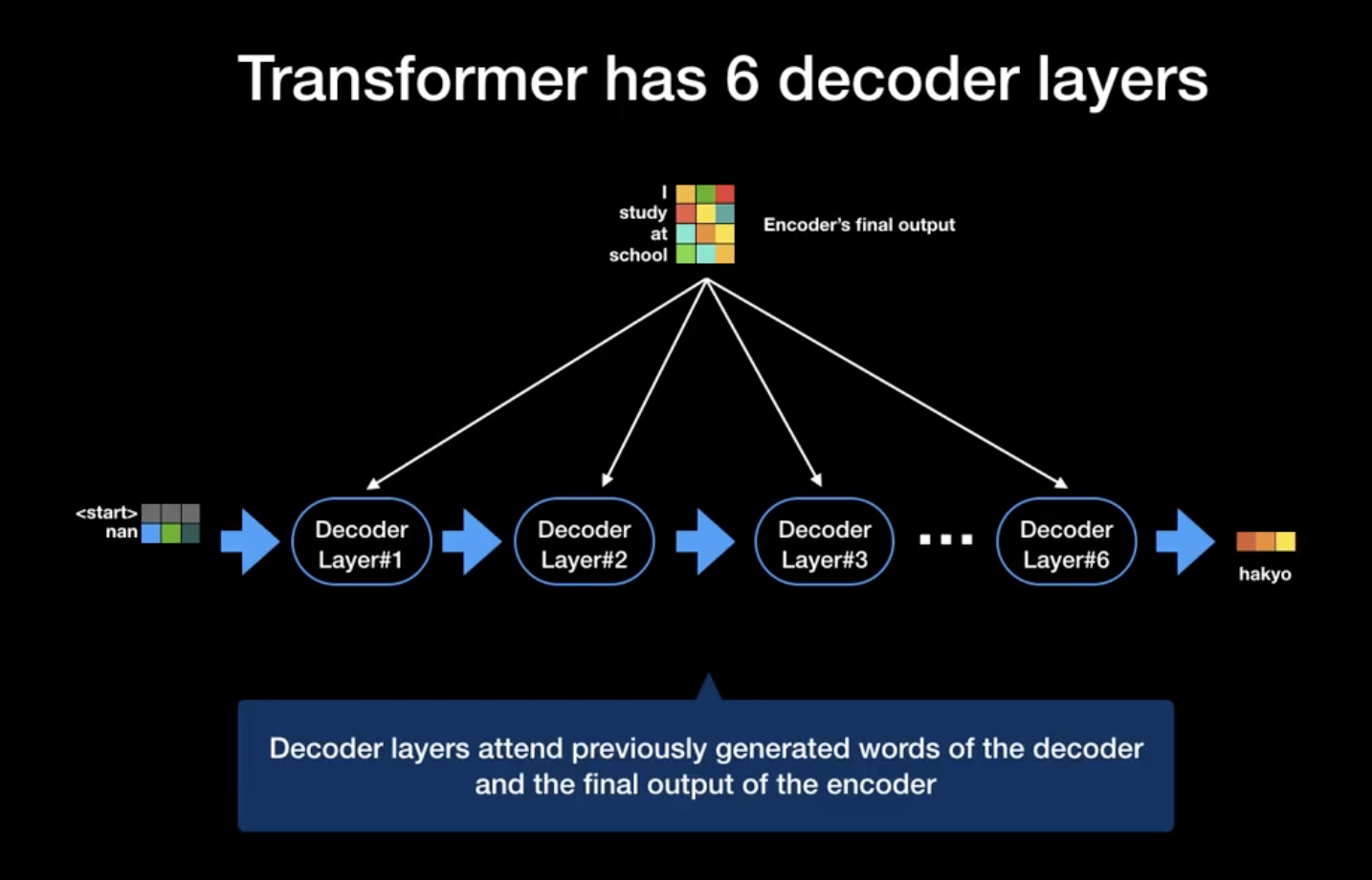
Decoder 역시 병렬식 처리를 적극 활용한다.
아래는 Attention is all you need의 자세한 설명이다.
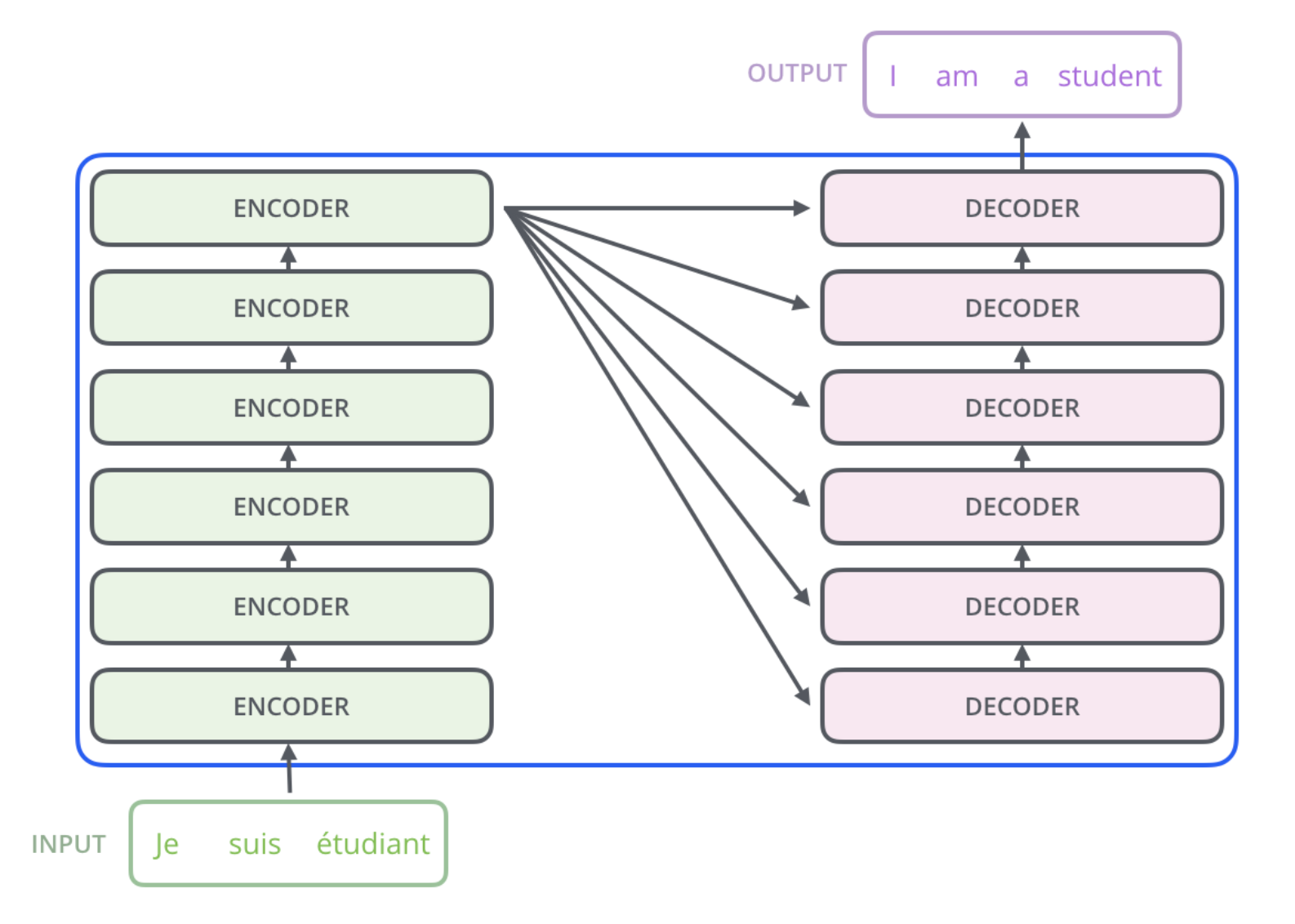
Encoding component : Encoding의 스택
Decoding component : Decoding의 스택(Encodig 스택 수와 같다.)
Encoding block vs Decoding block = Unmasked vs Masked
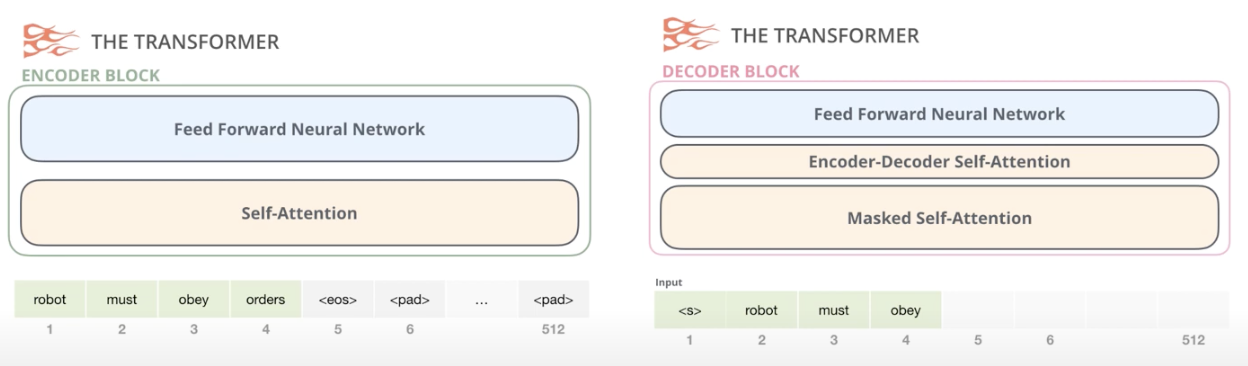
Transformer의 Encoder의 특징은 각각의 Encoder은 전부 동일한 구조를 가진다.
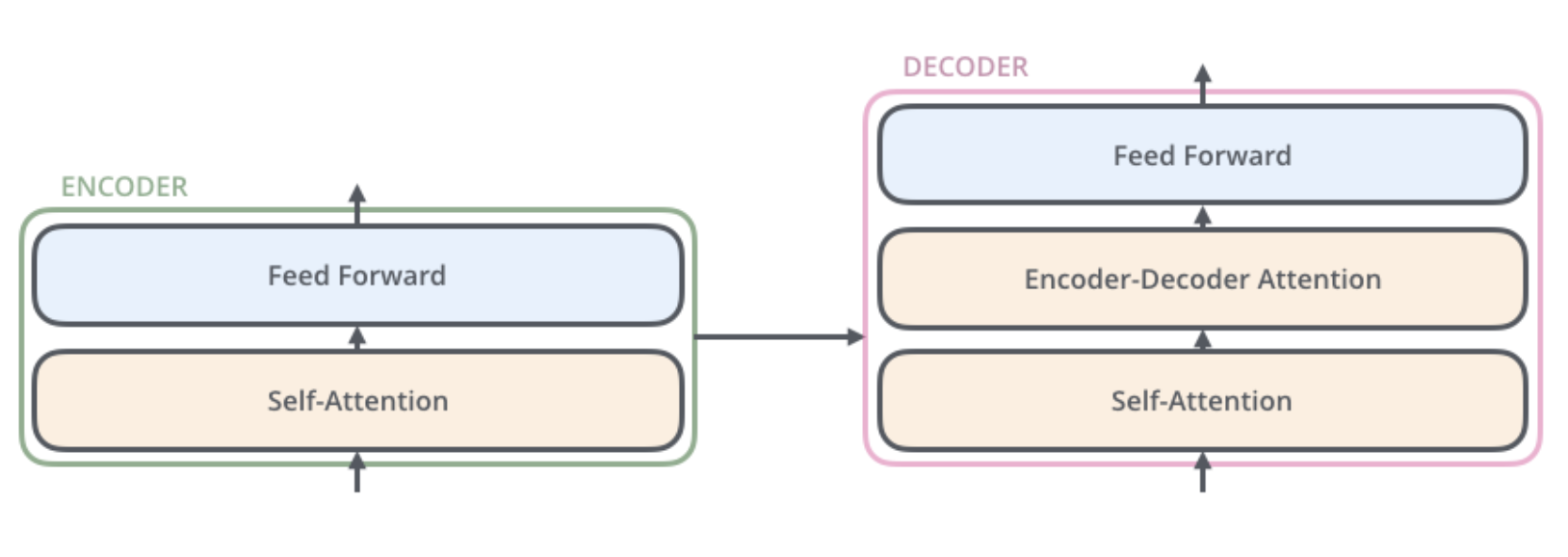
Encoder은Self Attention과 Feed Forward Neural Network로 구성되어 있다.
Decoder은 Encoder-Decoder Attention 레이어가 추가되어 있다.
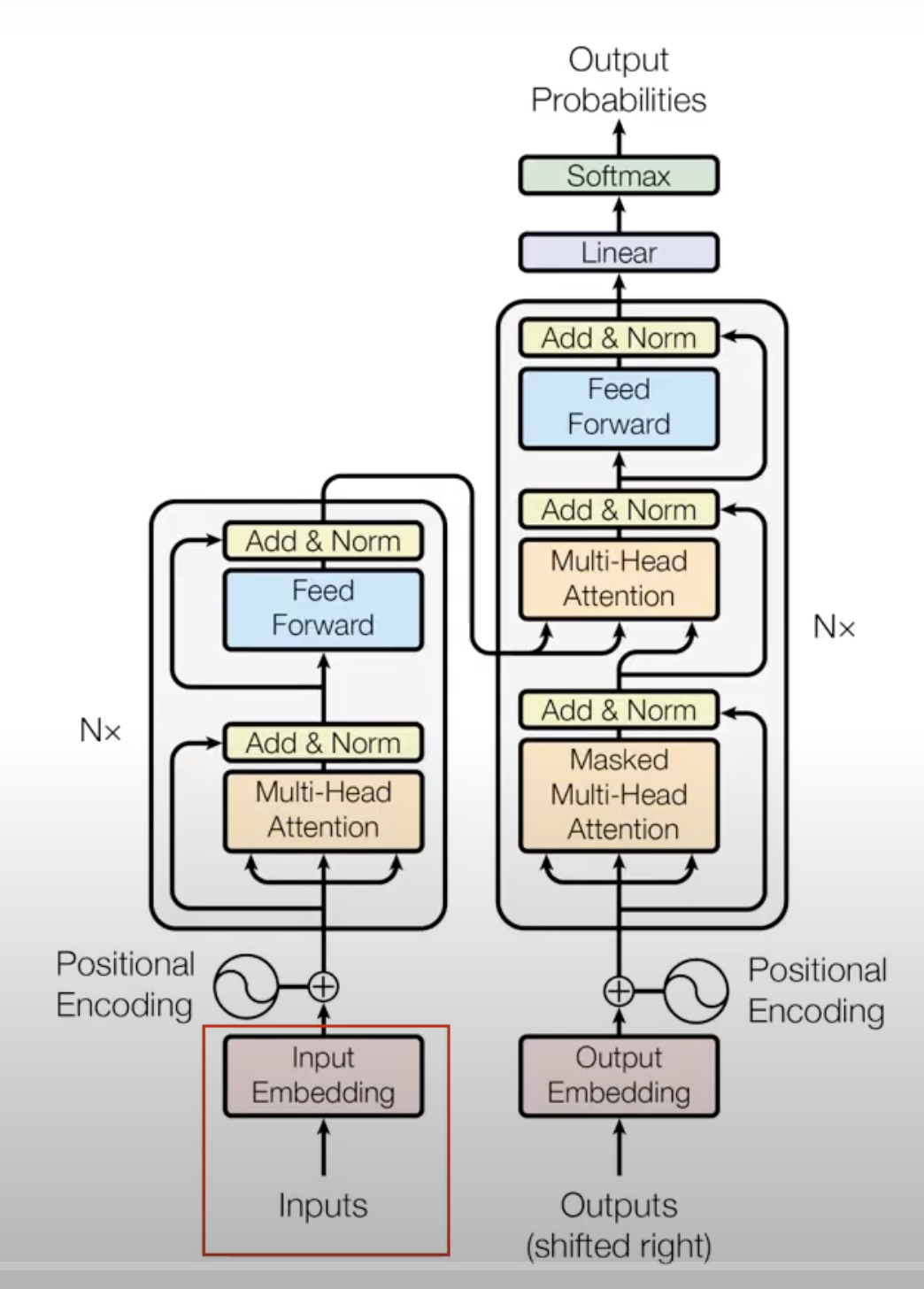
Encoder Block이 왼쪽, Decoder Block이 오른쪽이다.
Self Attention은 Single head attention이 아닌 Multi head attention이다.
Input Embedding : bottom-most encoder, 제일 첫번째 인코더의 input으로만 사용.
embedding algorithm을 통해 input embedding 수행(512 차원)
그 위의 encoder들은 바로 아래에 있는 encoder의 output을 input으로 받는다.(사이즈는 유지된다.)
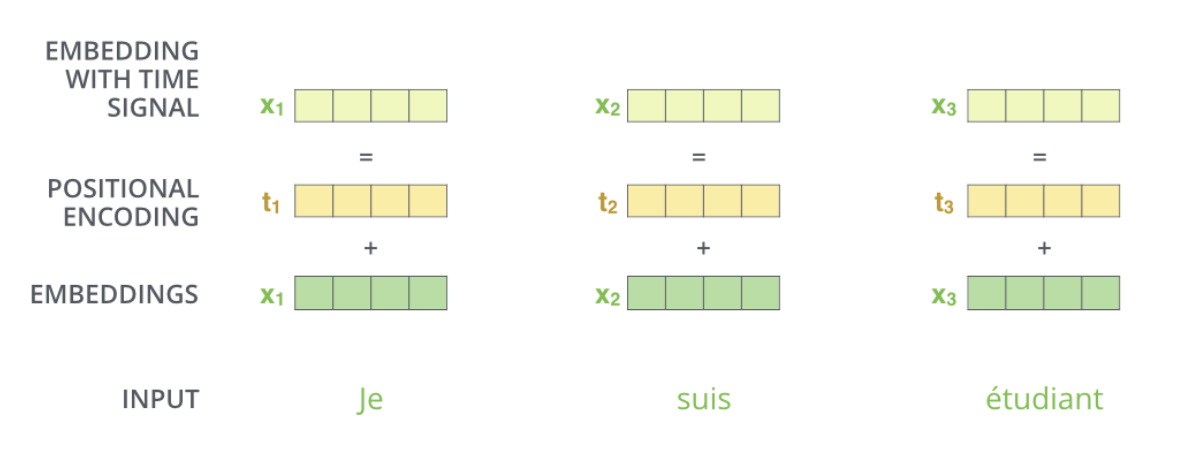
Positional Encoding : Input Embedding에 더하여(512차원의 벡터를 만듬/concat처럼 1024 차원이 되지 않음) 각각의 단어의 순서를 고려한다.
Positional Encoding을 왜하는가.
- 트랜스포머의 한번에 모든 sequence를 받기 때문에, 단어가 가진 위치정보를 고려하지 못하는 단점을 보완하는 장치이다.
-
해당하는 encoding의 size는 동일해야한다.
-
총 100개의 토큰들에 대해 512개 차원의 positional encoding을 해보면, L2 norm의 distribution은 평균 256, 표준편차 1.35가 나온다.
-> 위치 정보를 반영한다.
Imbedding된 단어들은 이제 Encoder의 2개의 Layer를 지나간다.
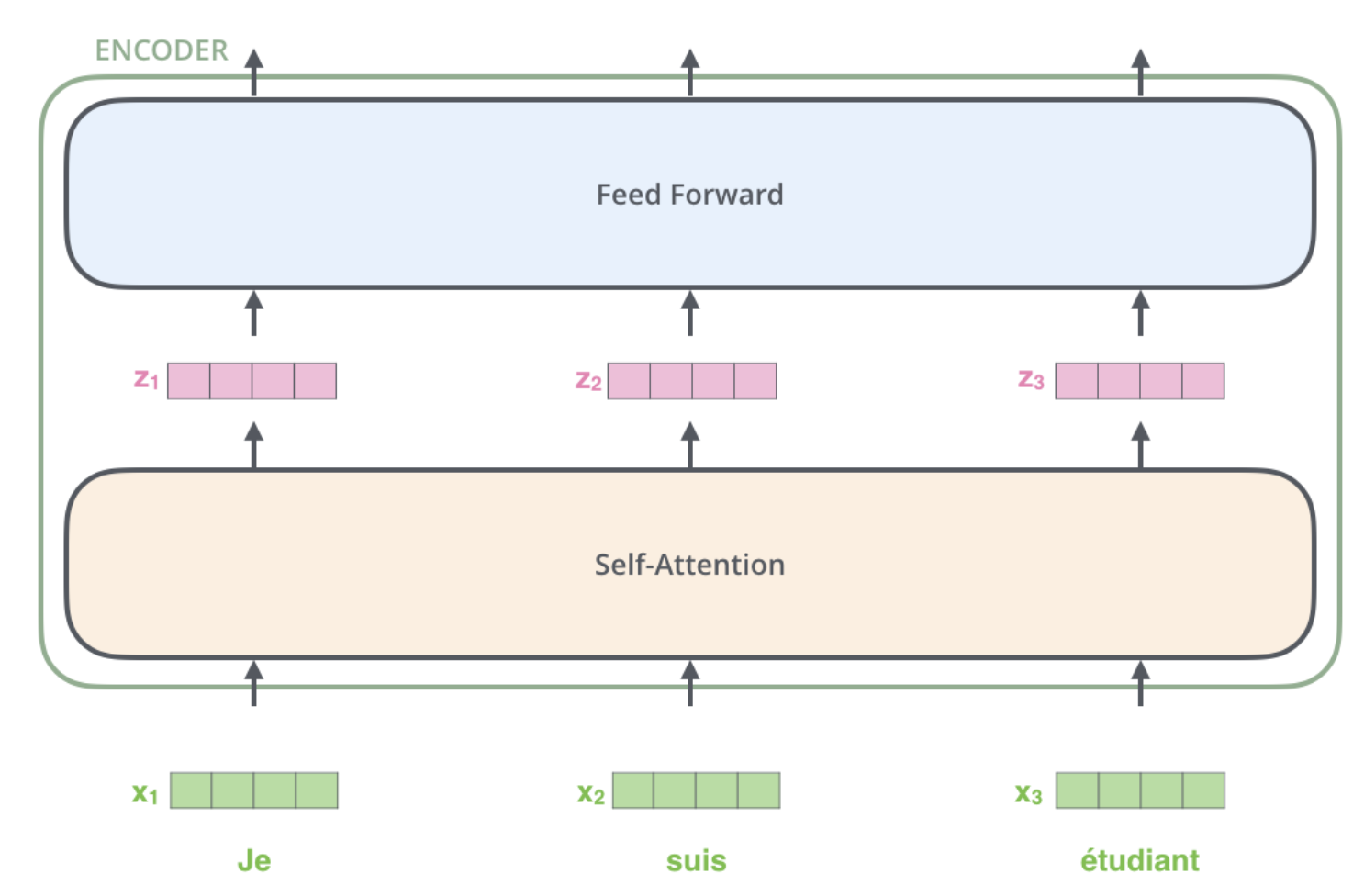
위의 4차원 벡터들이 self-attention layer을 지나면 4차원의 벡터가 들어가는데, self-attention layer은 dependency가 있고, Feed-Forward는 dependency가 없다.
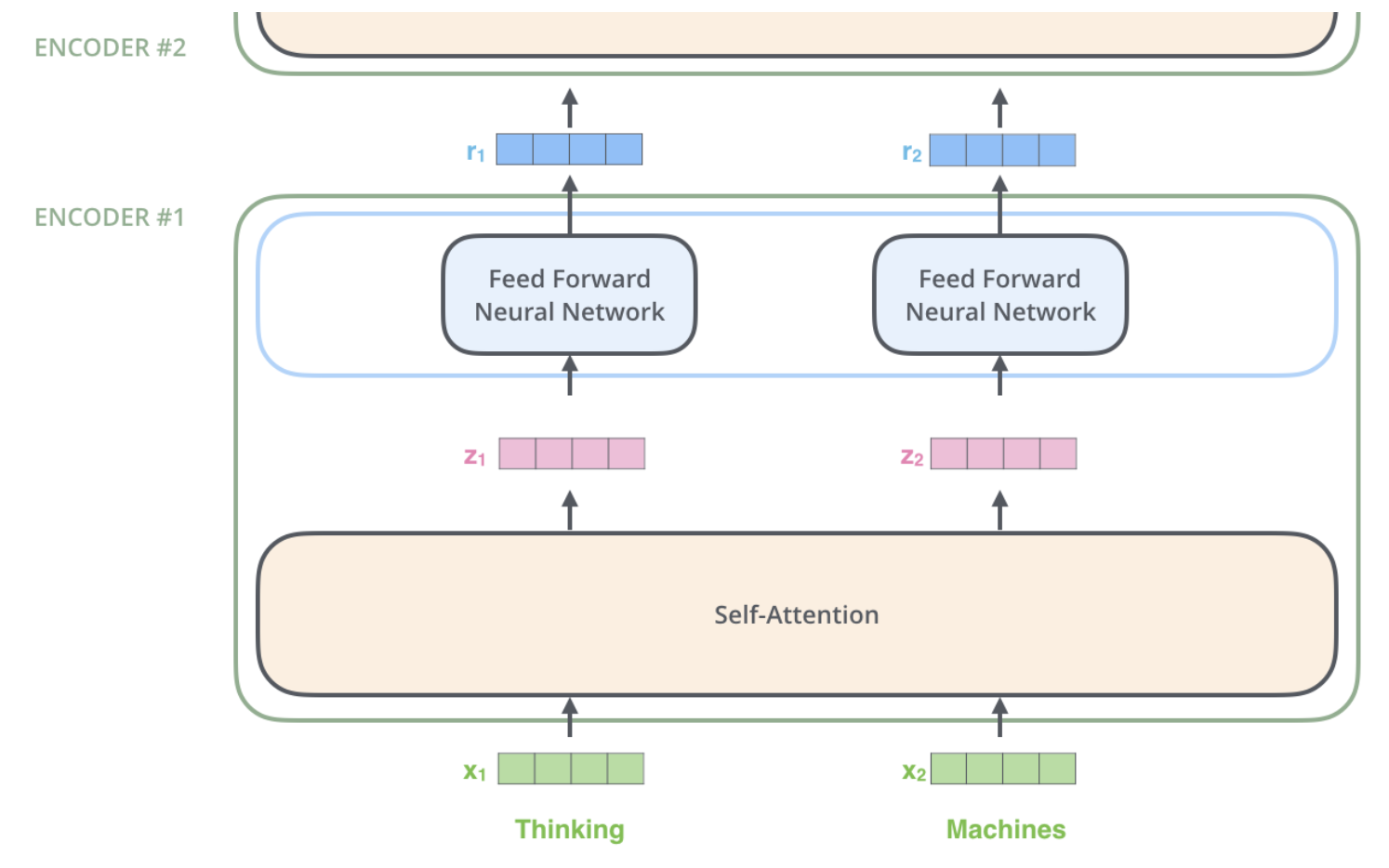
첫번째 encoder의 출력값인 r1과 r2는 두번째 encoder에 input으로 사용된다.
Self-Attention
3가지의 벡터가 필요하다.
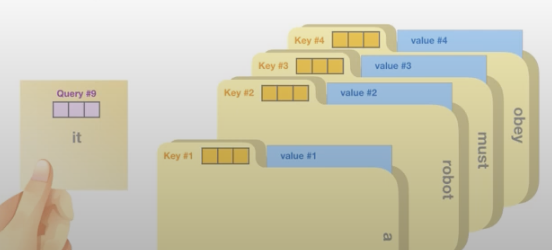
- Query : 현재 보고 있는 단어의 representation, 다른 단어들을 score하기 위한 기준
- Key : label, relevant word를 찾을 때 참고할 수 있는 폴더와 같은 역할
- Value : 실제 값
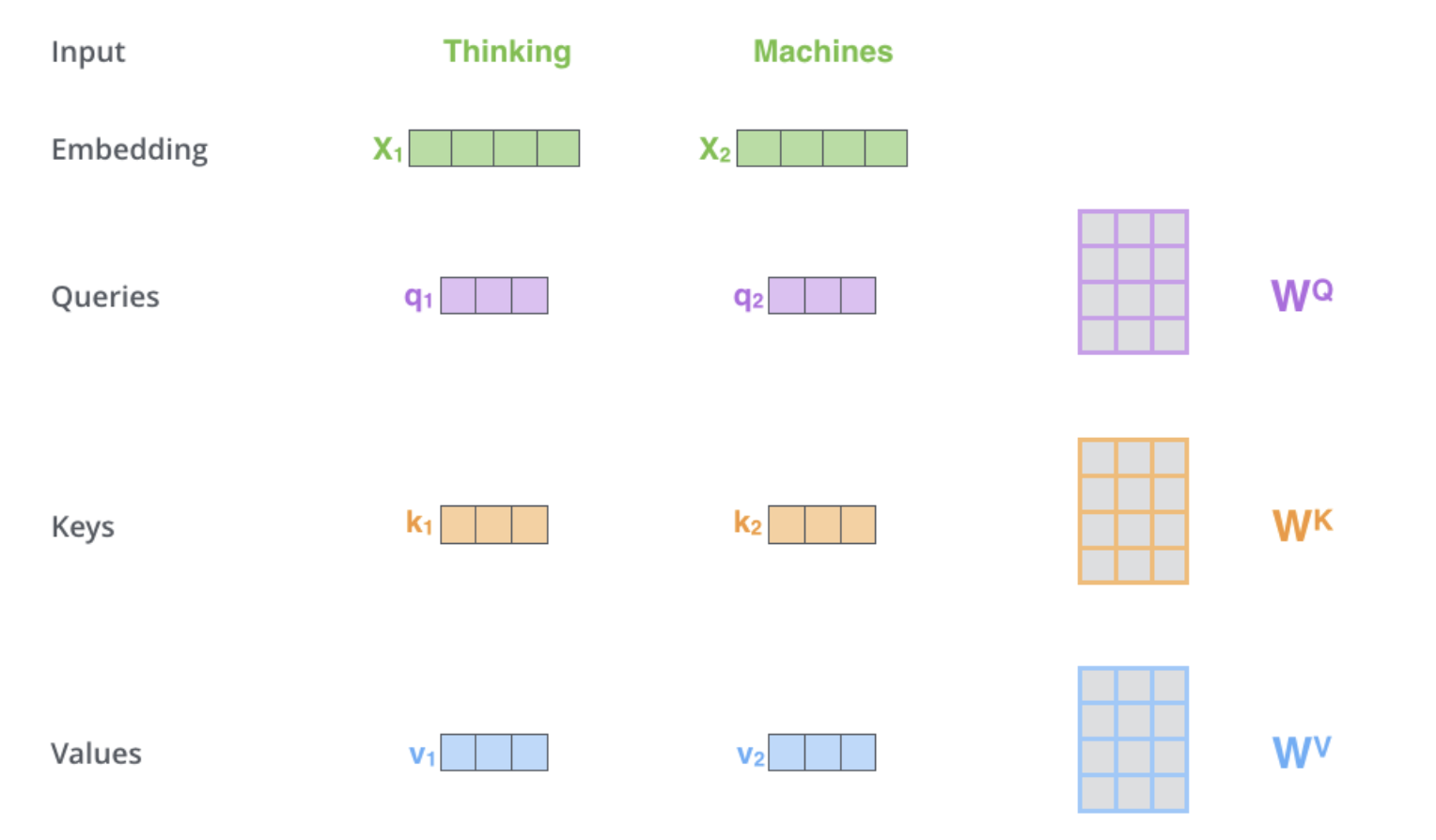
Step 1
$X_1$(1x4)과 $W^Q$(4x3)와 내적하여 $q_1$(1x3) … 로 Queries, Keys, Values를 생성한다.
일반적으로 input dimension보다는 Queries, Keys, Values의 dimension을 적게잡는다.
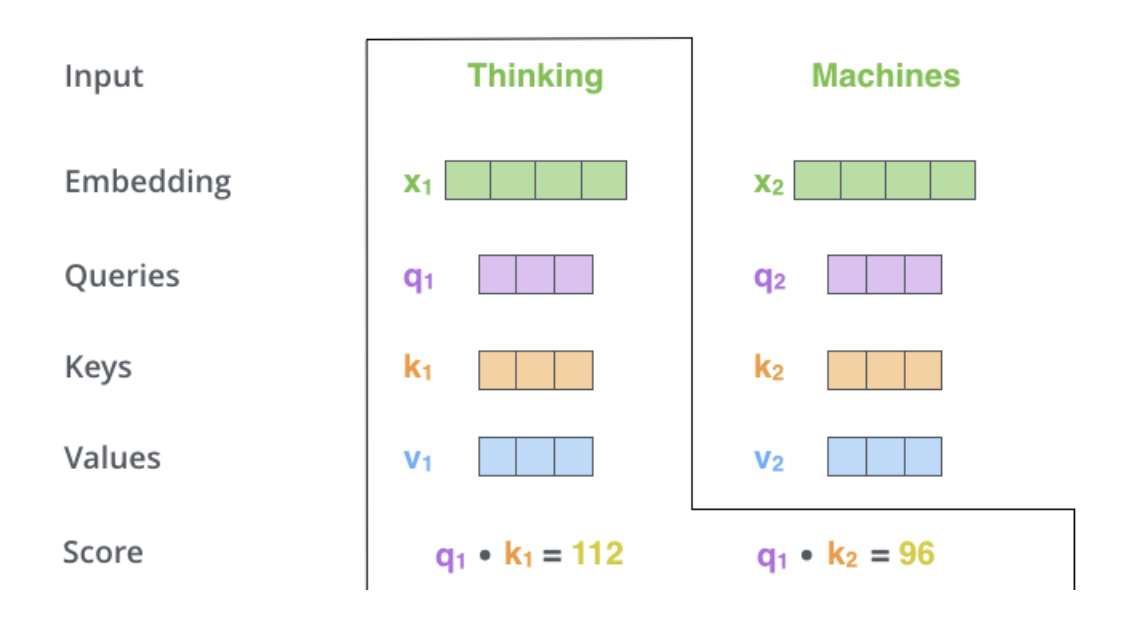
Step 2
현재 보고 있는 토큰의 Query($q_1$)와 나머지 key value($k_1, k_2$)를 곱해준다.
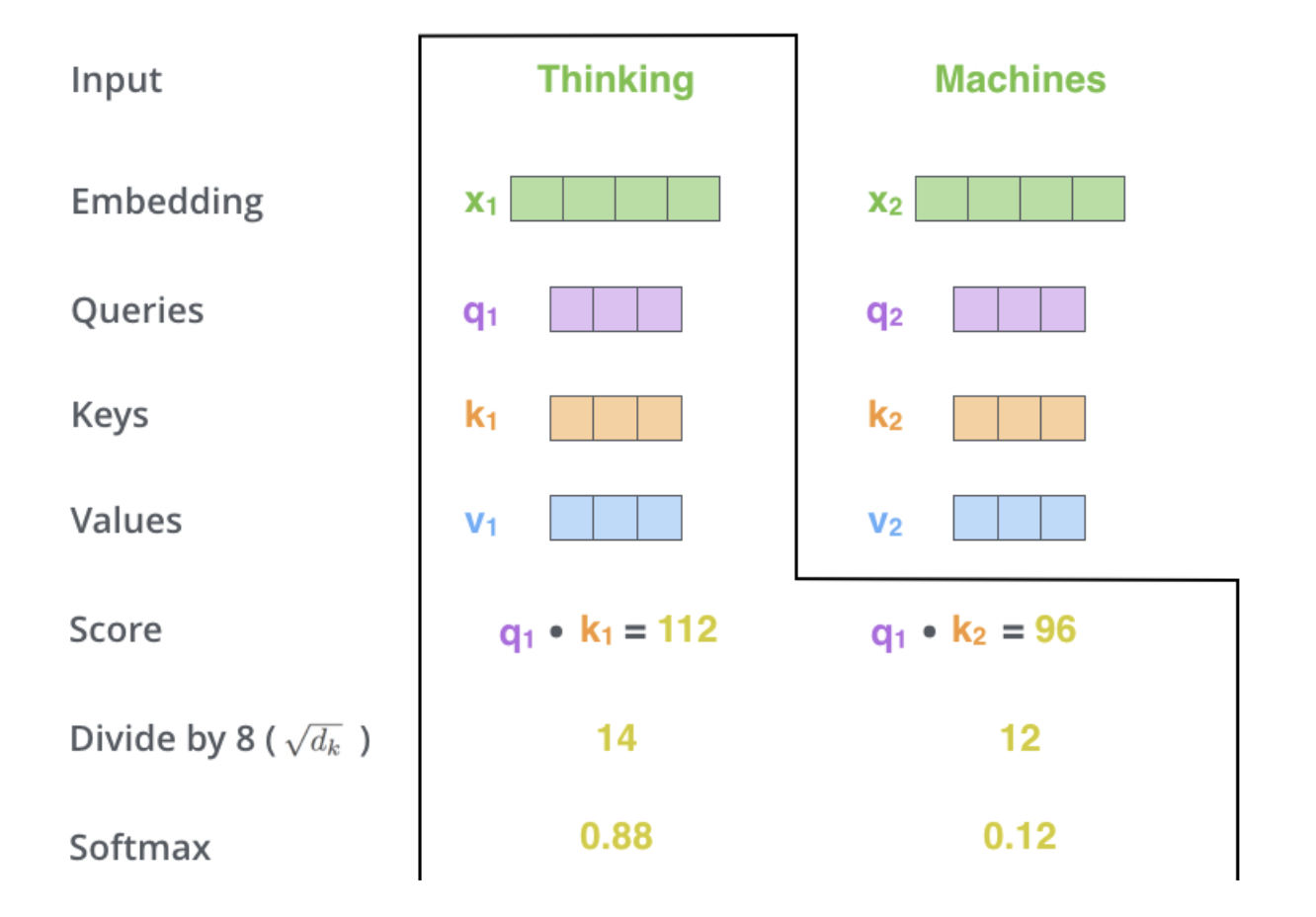
Step 3
$\sqrt{d_k}$를 Score에 나눠준다.
Step 4
이 값을 Softmax를 처리한다.
해당 값은 현재 position의 단어가, 얼마나 중요한 역할을 하는가에 대한 지표
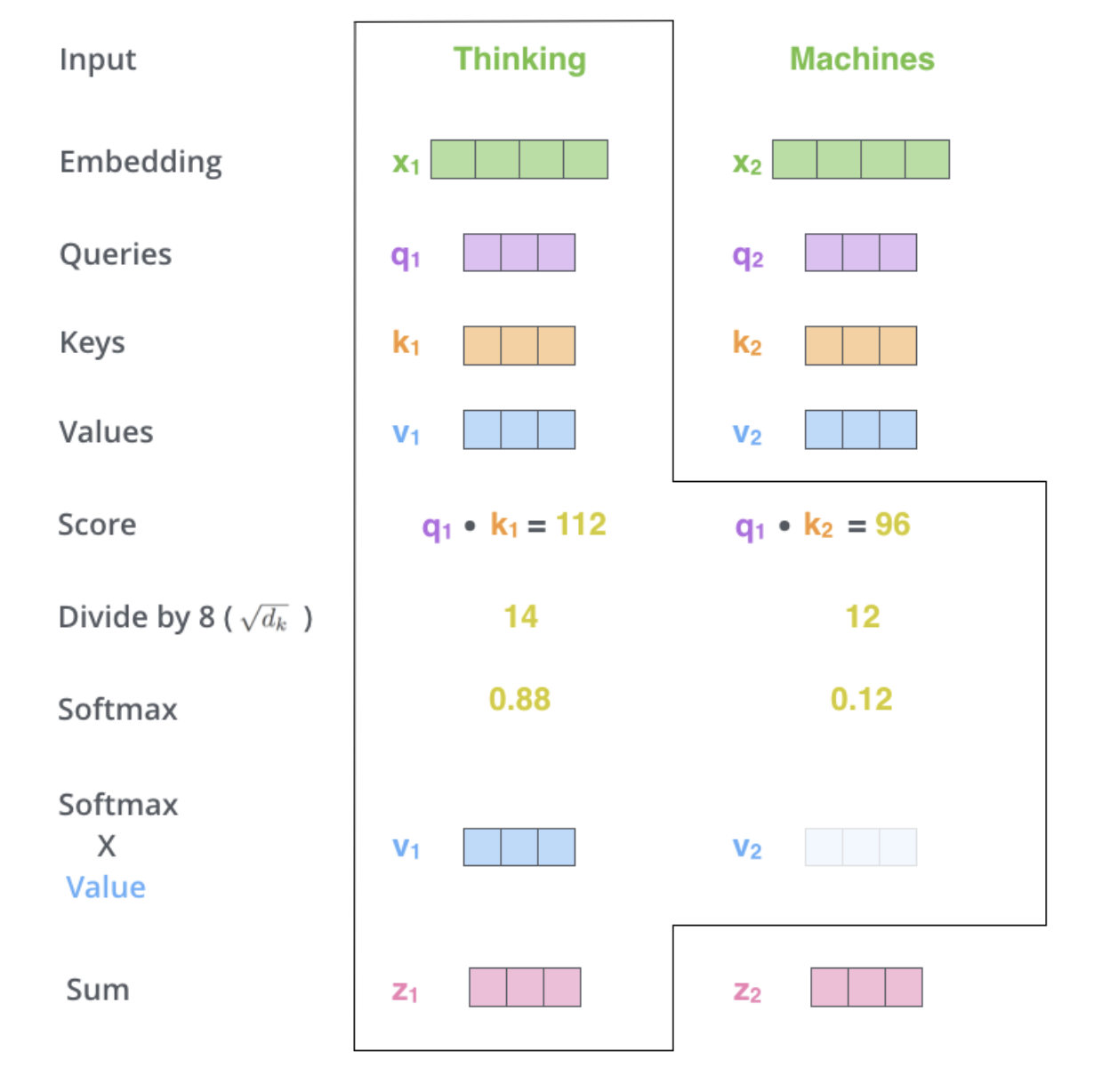
Step 5
파랑색의 $v_1$은 원래의 $v_1$에 softmax를 곱한 값이고,
파랑색의 $v_2$은 원래의 $v_2$에 softmax를 곱한 값이다.
Step 6
$z_1$ 은 $v_1$과 $v_2$를 더한 값(가중 합이 된)이다.
이 값이 self attention의 output이다.
이를 Matrix calculation으로 보면 아래와 같다.
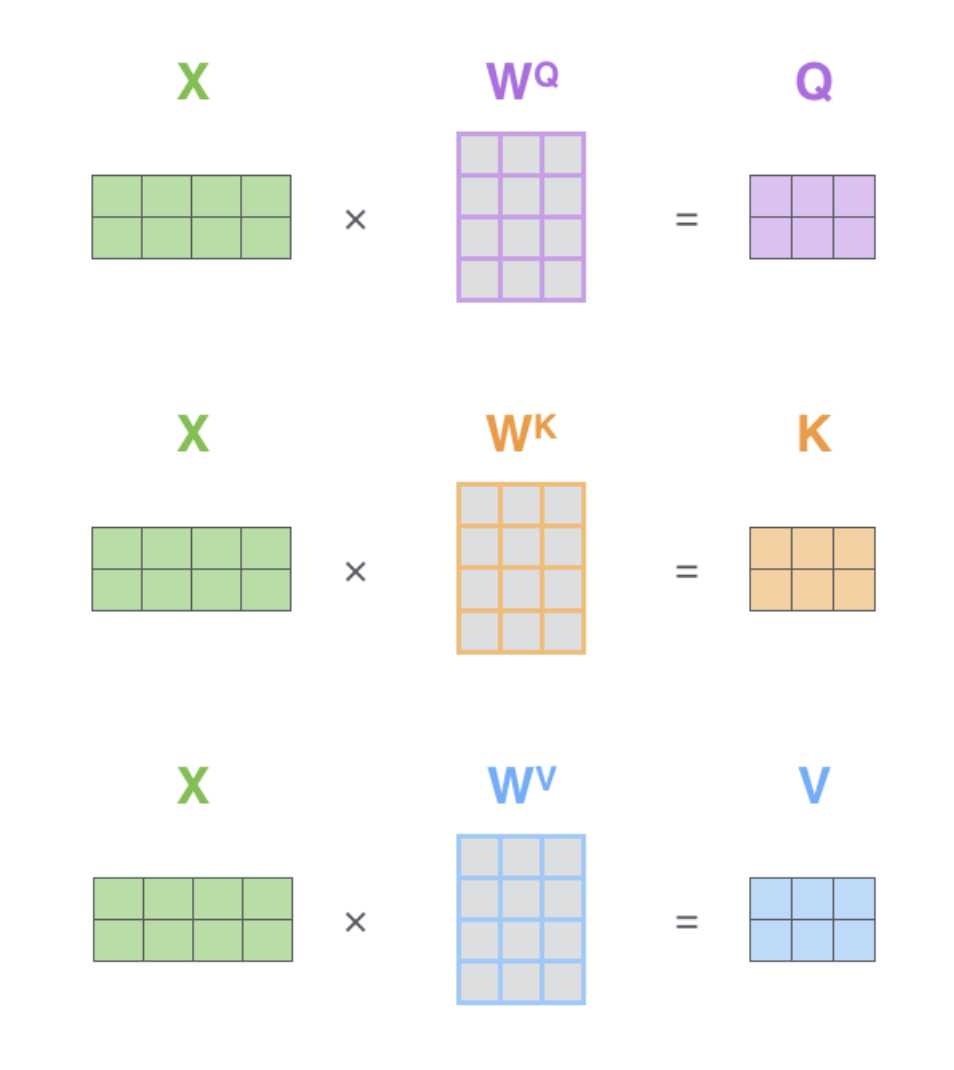
이 Matrix를 통해 Z 값을 같는 수식을 표현하면 아래와 같다.
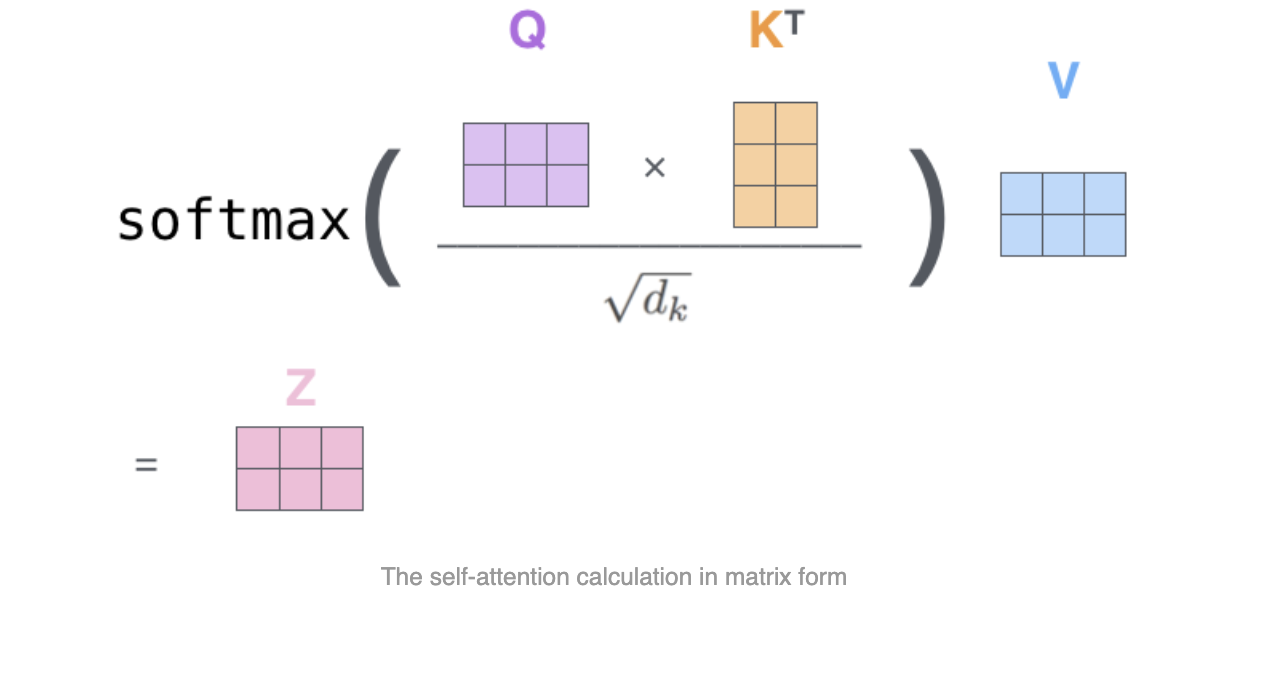
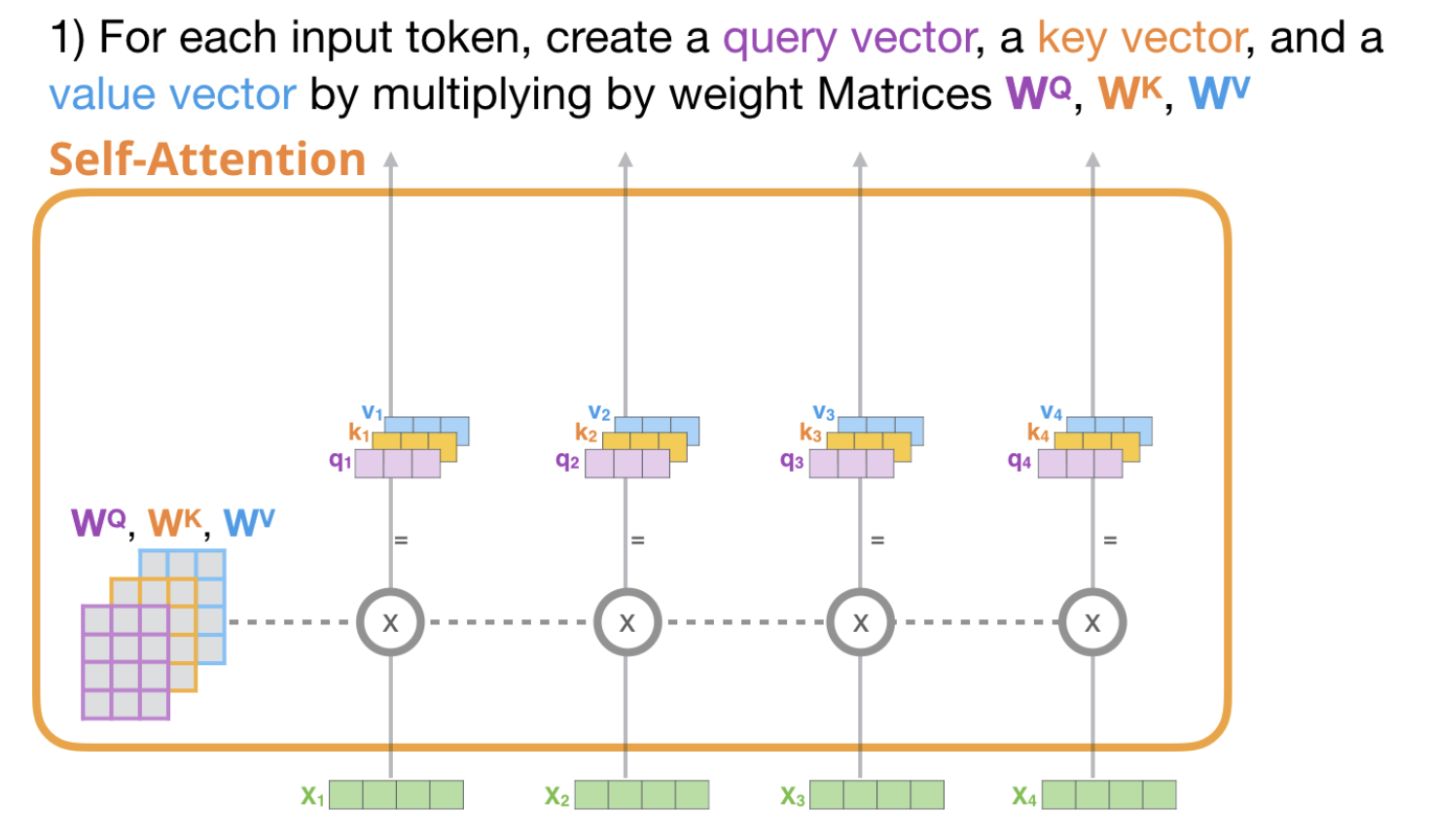
각각의 $x$ 벡터에 대해 $q,k,v$가 계산을 할 수 있다.
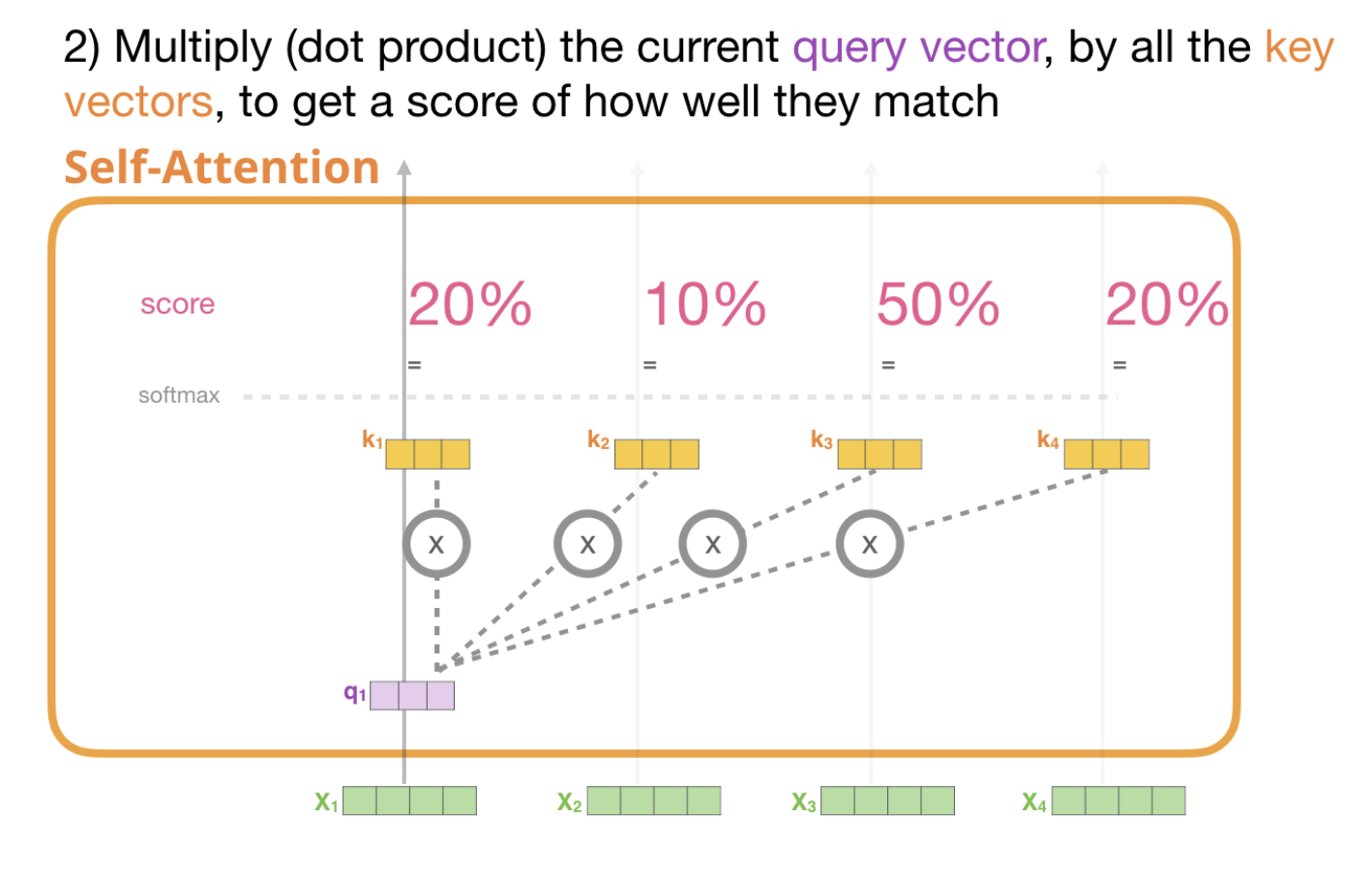
이를 바탕으로 첫번째 $q_1$에 대해 $k_1, k_2, k_3, k_4$에 대해 곱셈을 한 뒤에, Softmax를 취하여 가중치를 구한다.
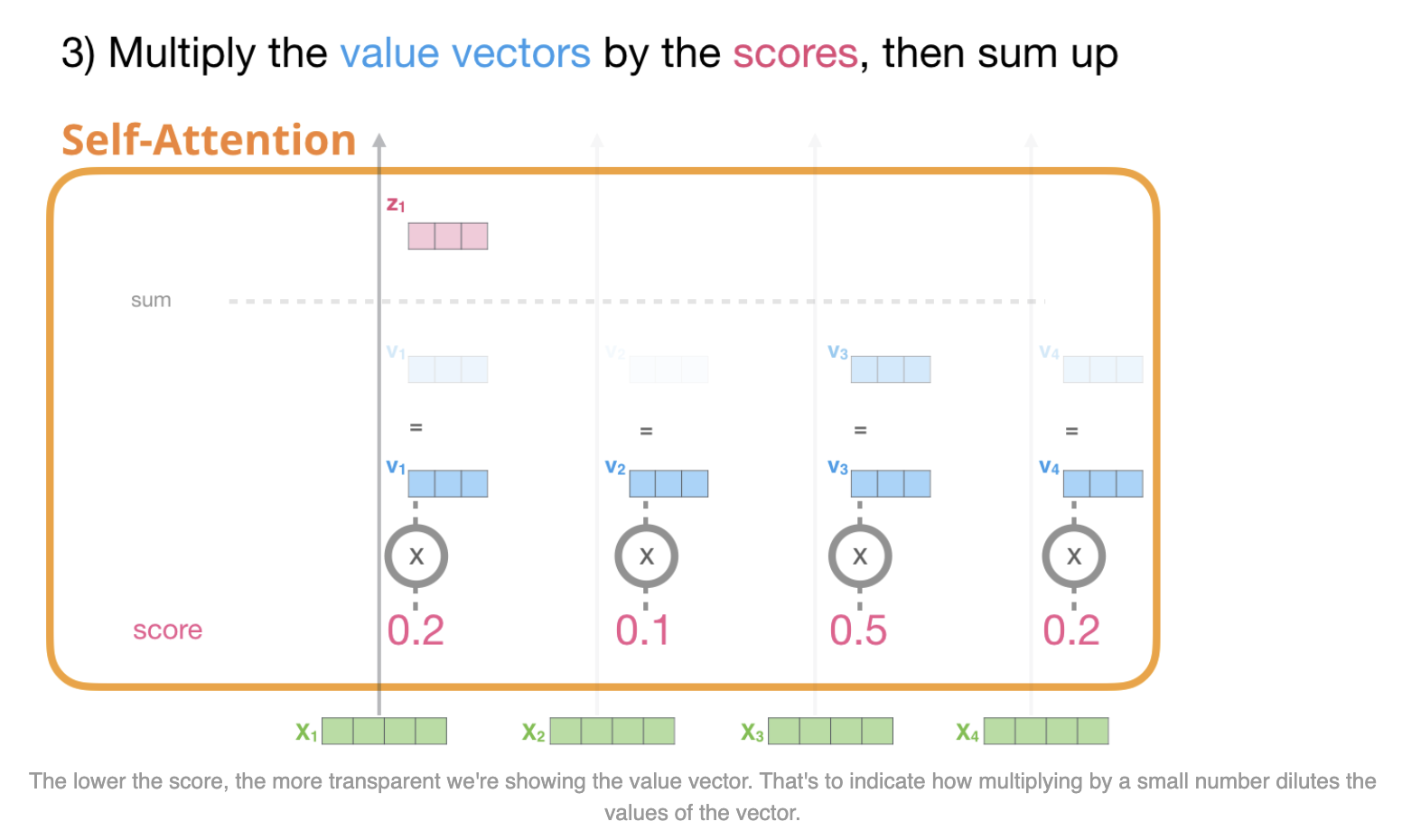
이런 가중치를 value 값을 곱한 후, 합쳐서 $z_1$을 구한다.
지금까지 구한 과정은 ‘single attention’이다.
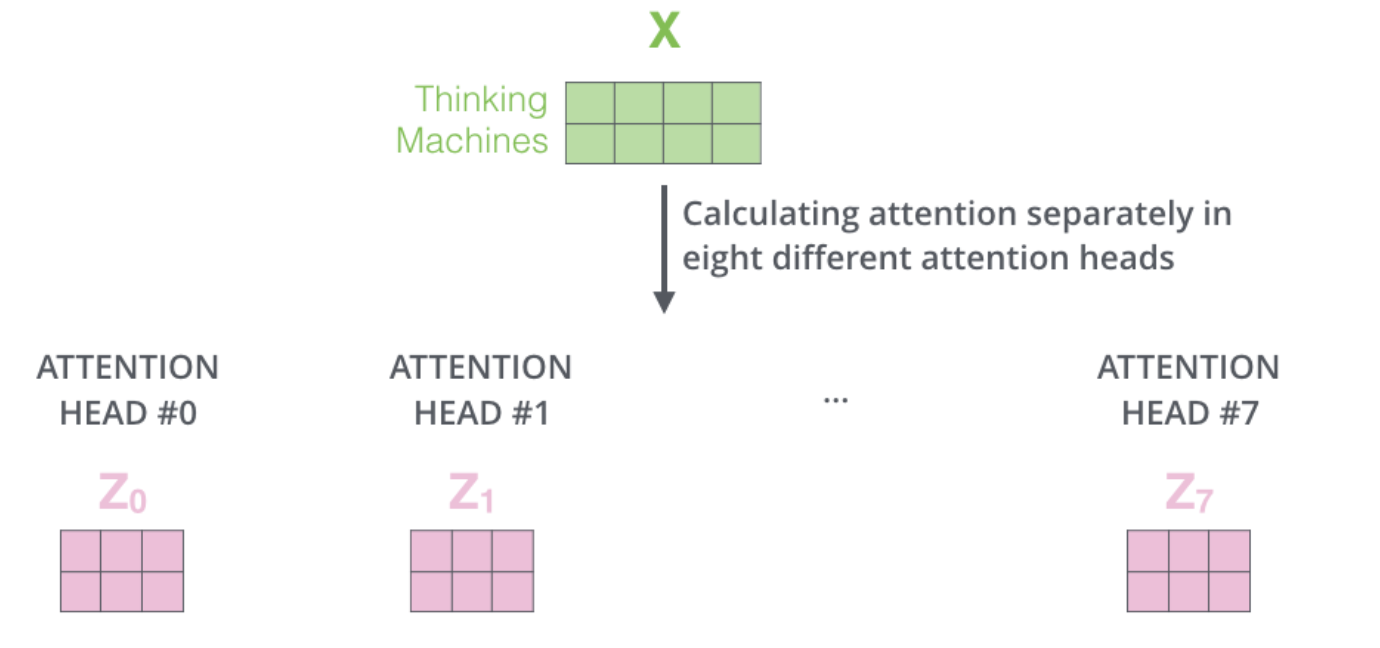
‘Multi-headed attention’은 다른 여러 개의 Attention Head을 사용한다.
-> $z$값도 여러 값이 나온다.

모든 $z$값을 모두 concatenate한다.
이 z값의 행의 갯수(24)와 같은 갯수의 column을 가지고, input embedding과 같은 차원의 행을 가지는 $W^0$를 설계한다.
이를 통해 계산한다면, 처음 input embedding과 동일한 차원의 $Z$값을 산출할 수 있다.
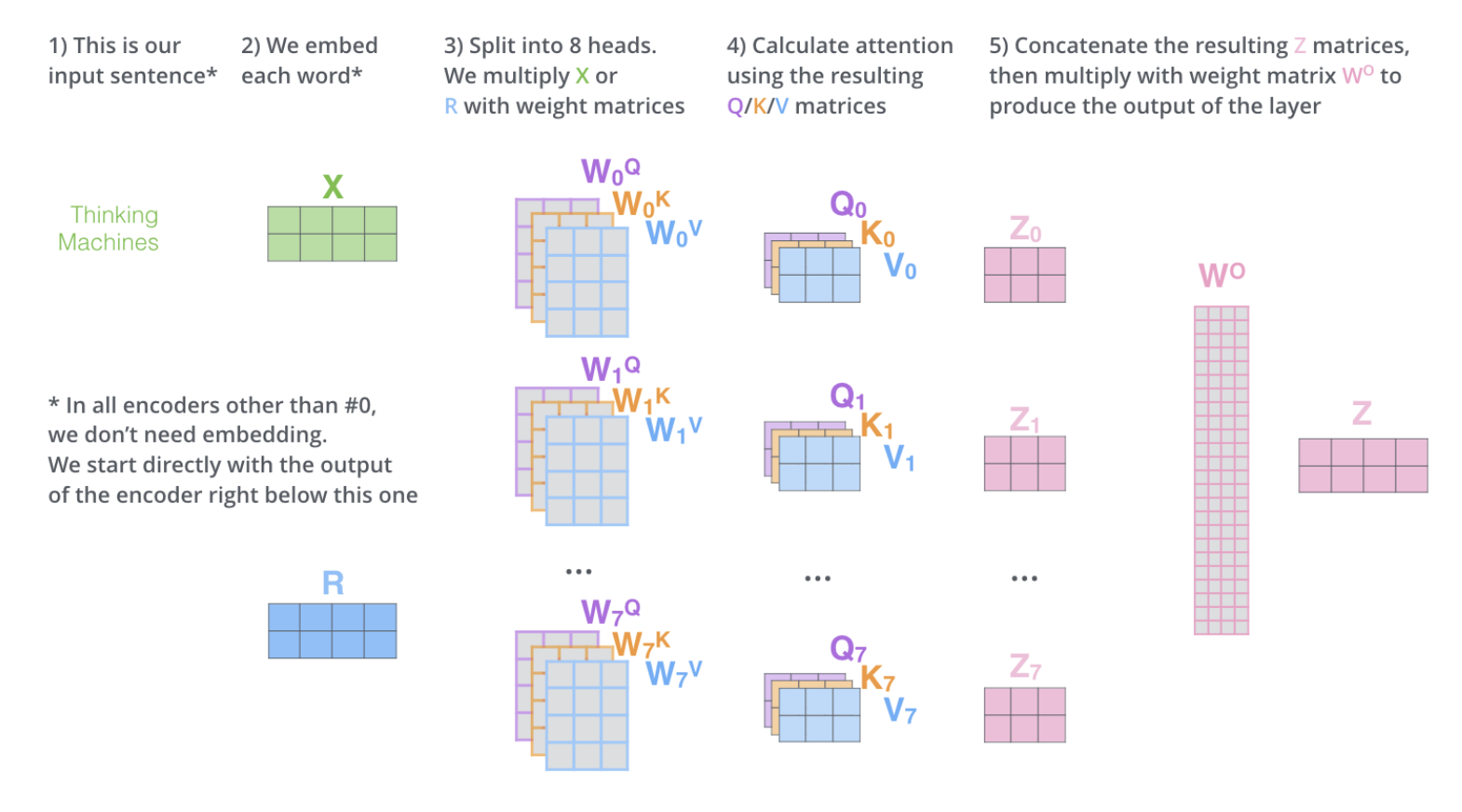
이를 간략하게 보면 위와 같다.
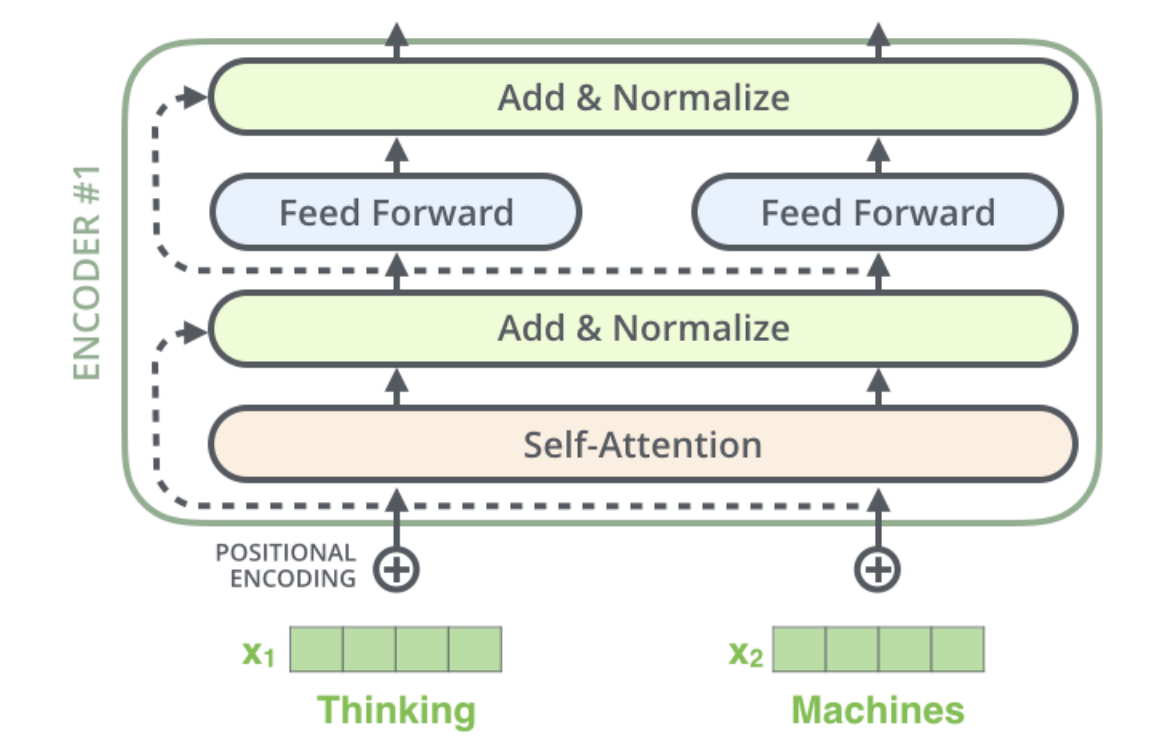
Encoder은 이렇게 Self-Attention한 결과에 대해서 Residual block을 ‘Add’하고, ‘Normalize’한다.
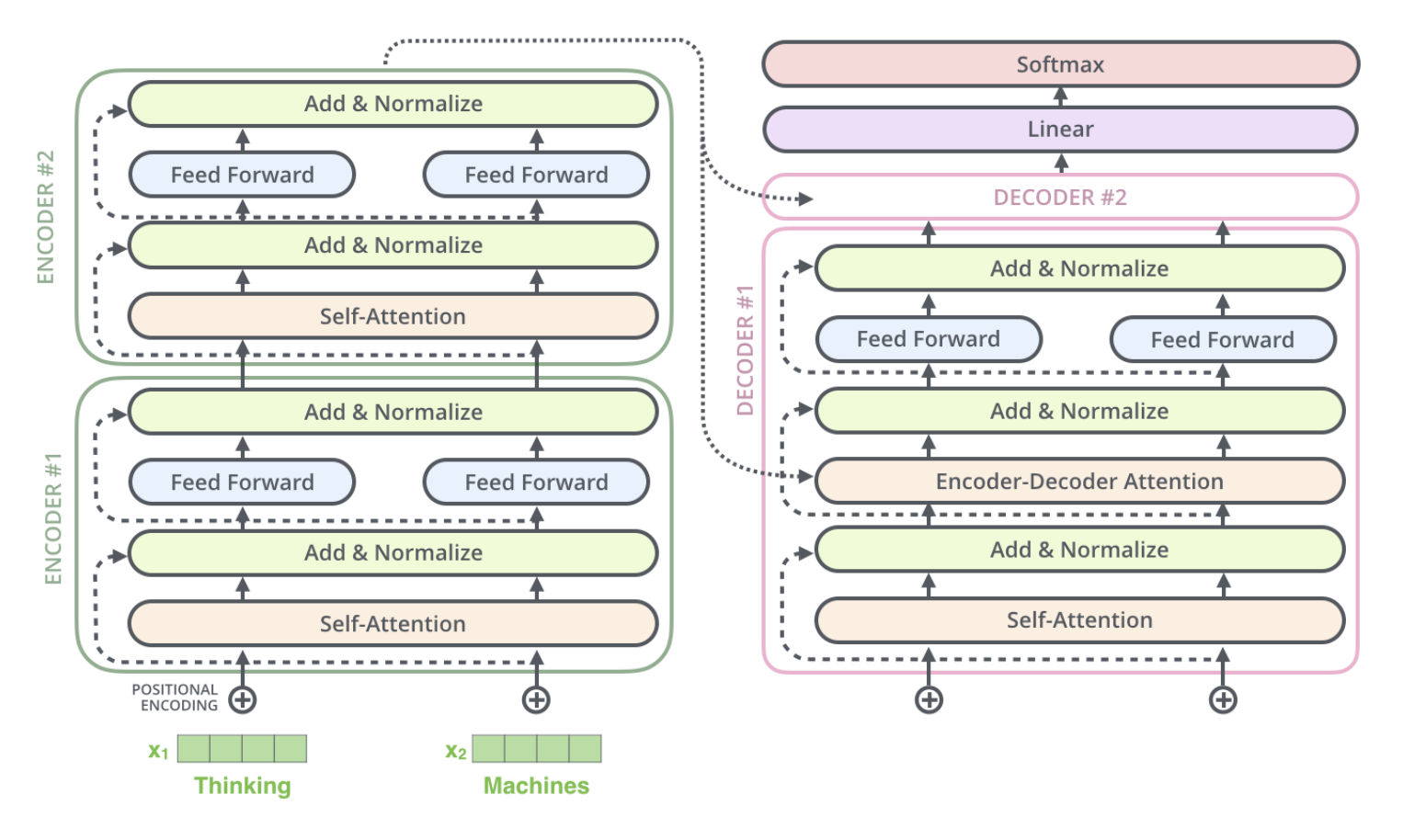
Encoder 뿐만 아니라, Decoder에서도 Residual block을 ‘Add’하고, ‘Normalize’한다.
이 값을 마지막으로 encoder를 통과시키는 것은 Feed Forward Network이다.
Feed Forward
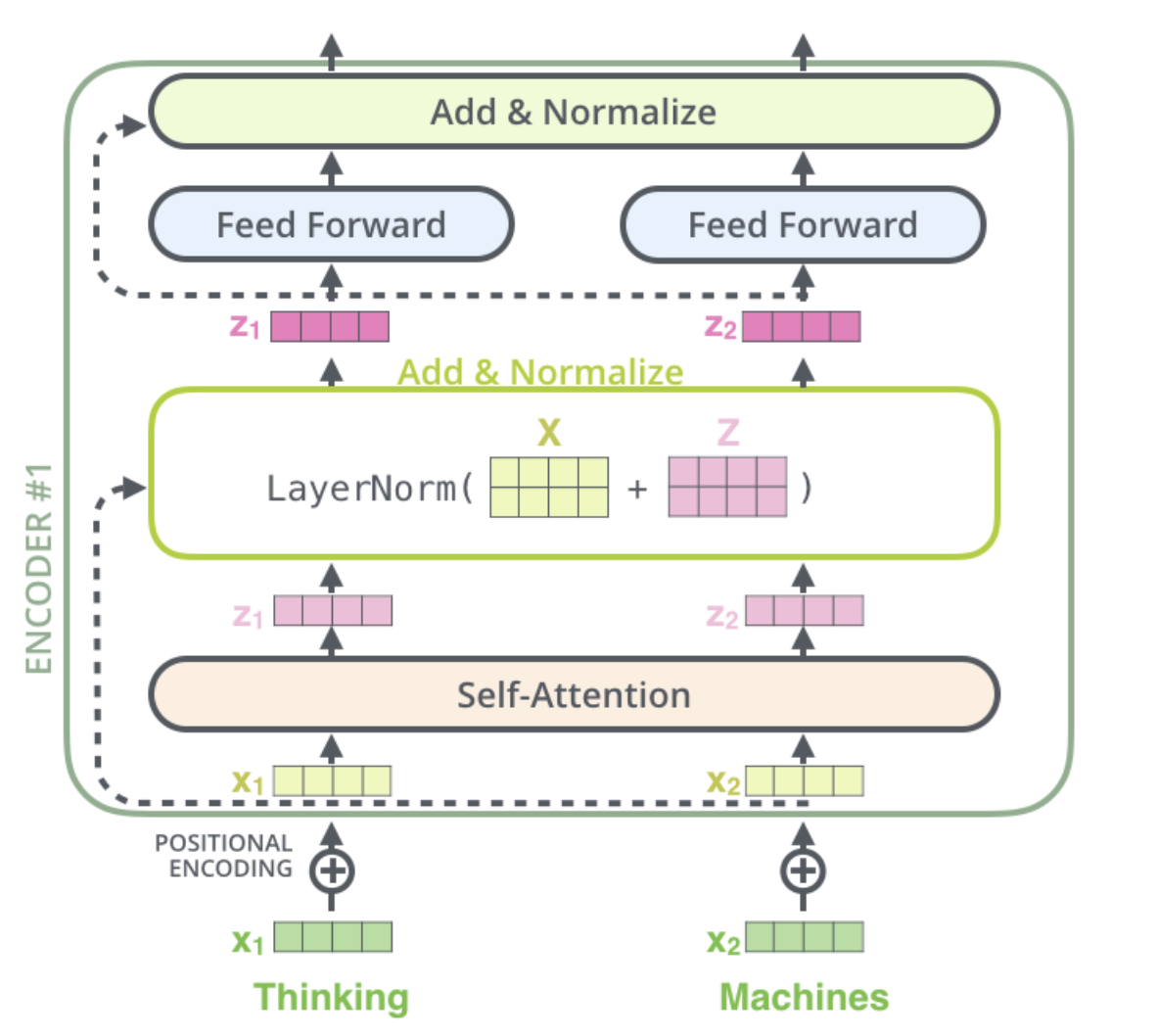
Feed Forward Network
- Fully connected feed-forward network
- Self Attention과 Residual block Add, Normalize가 끝난 z값을 Feed Forward에 통과시킨다.
- 각각의 포지션에 대해 개별적으로 적용한다.
- 각각의 layer마다 다른 파라미터를 사용한다.
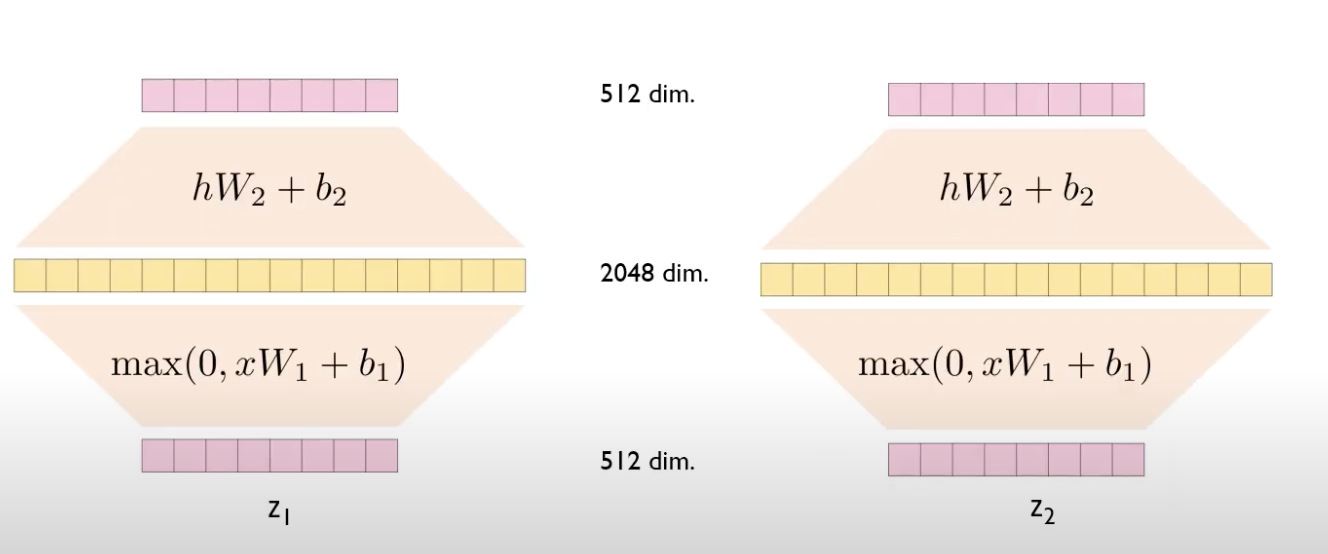
$z_1$과 $z_2$를 다른 neural network를 각각 이용한다.
같은 block 내에서는 동일한 파라미터를 이용한다.
($W_1$, $W_2$는 왼쪽, 오른쪽 같다.)
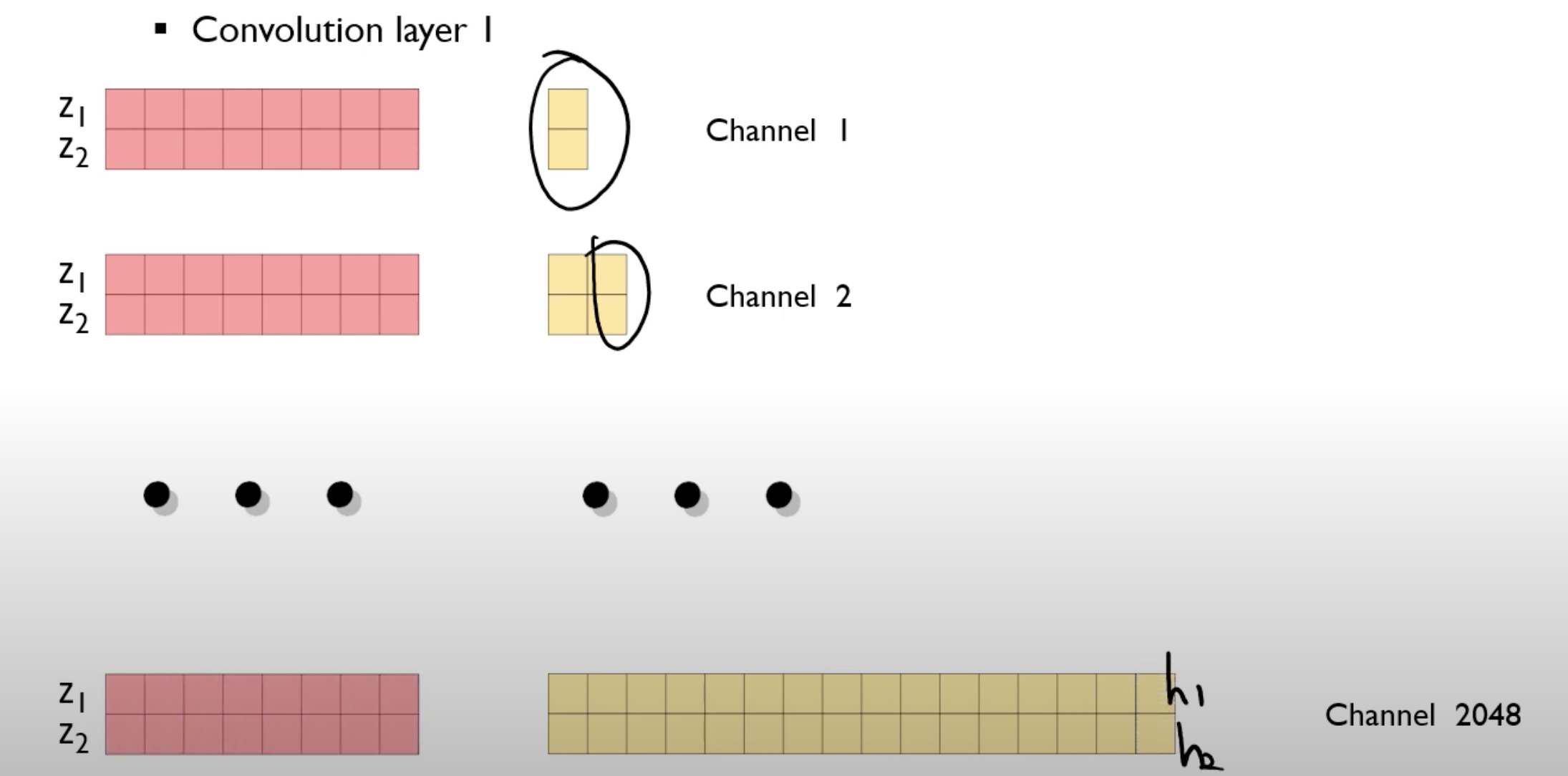
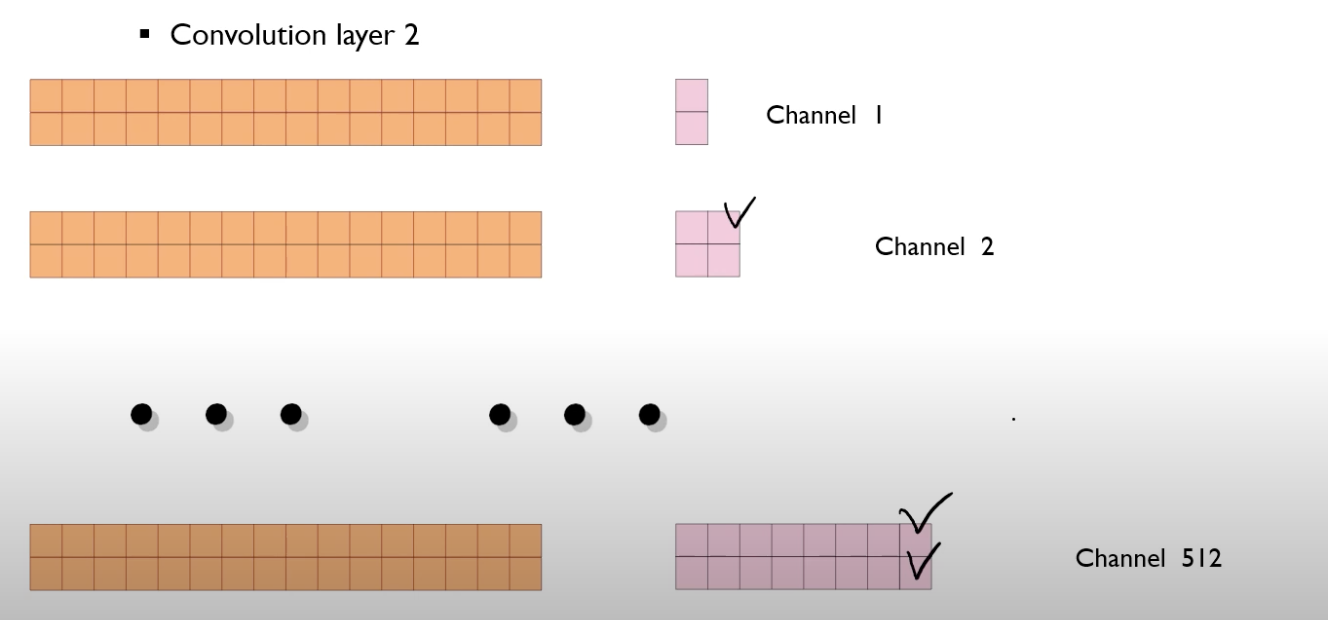
결국은 convolution 연산의 개념을 도입하면 NN 계산을 빠르게 수행할 수 있다.
이제 Decoder에 대해서 보면

먼저 Masked Multi-Head Attention가 나온다.
Decoder의 self attention은 반드시 자기 자신보다 앞쪽의 포지션에 대해서만 토큰들의 어텐션만 볼 수 있다.
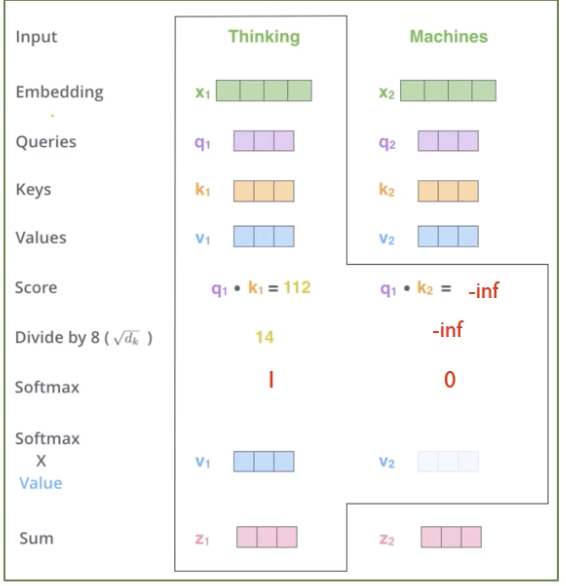
이를 수식적으로 표현하기 위해서 $-inf$로 masking해줘 softmax을 1,0으로 할당한다.
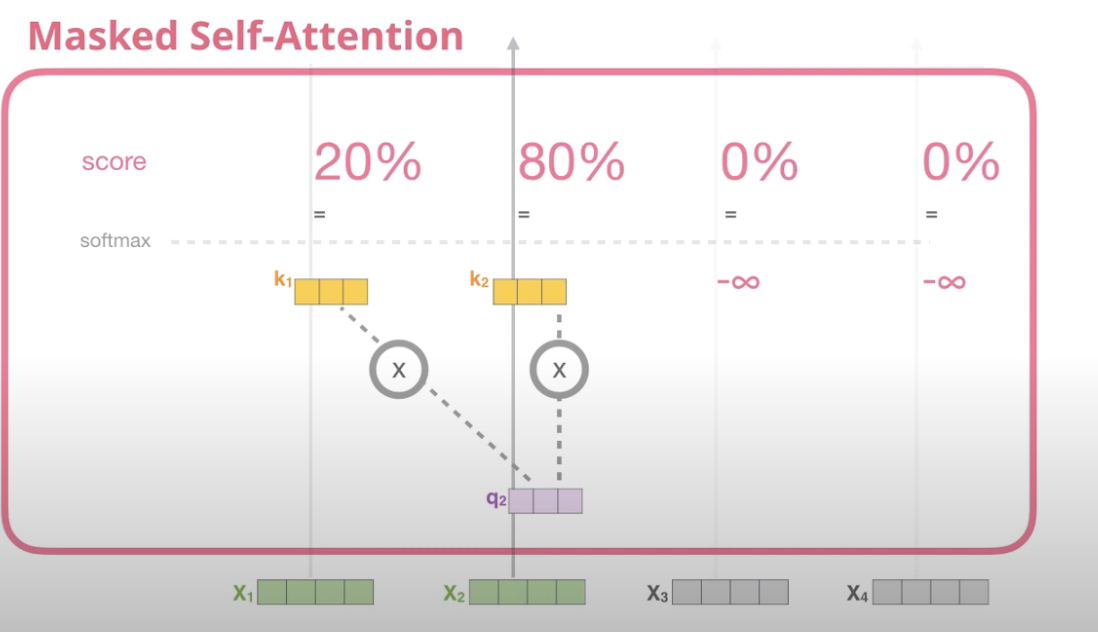
이를 다른 그림으로 보면, 뒤의 score은 모두 0으로 할당된 것을 볼 수 있다.

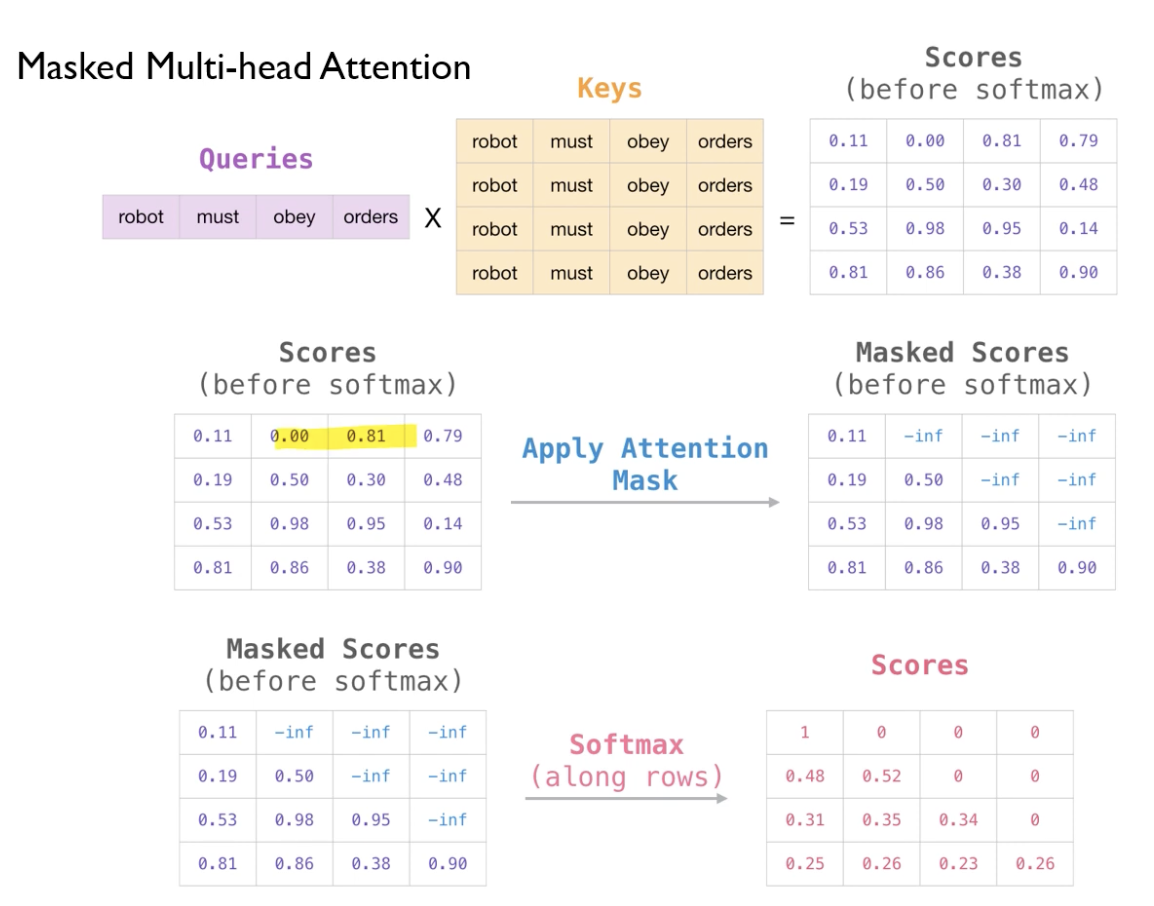
score에서 masking 된 부분이 모두 0으로 된 것을 볼 수 있다.
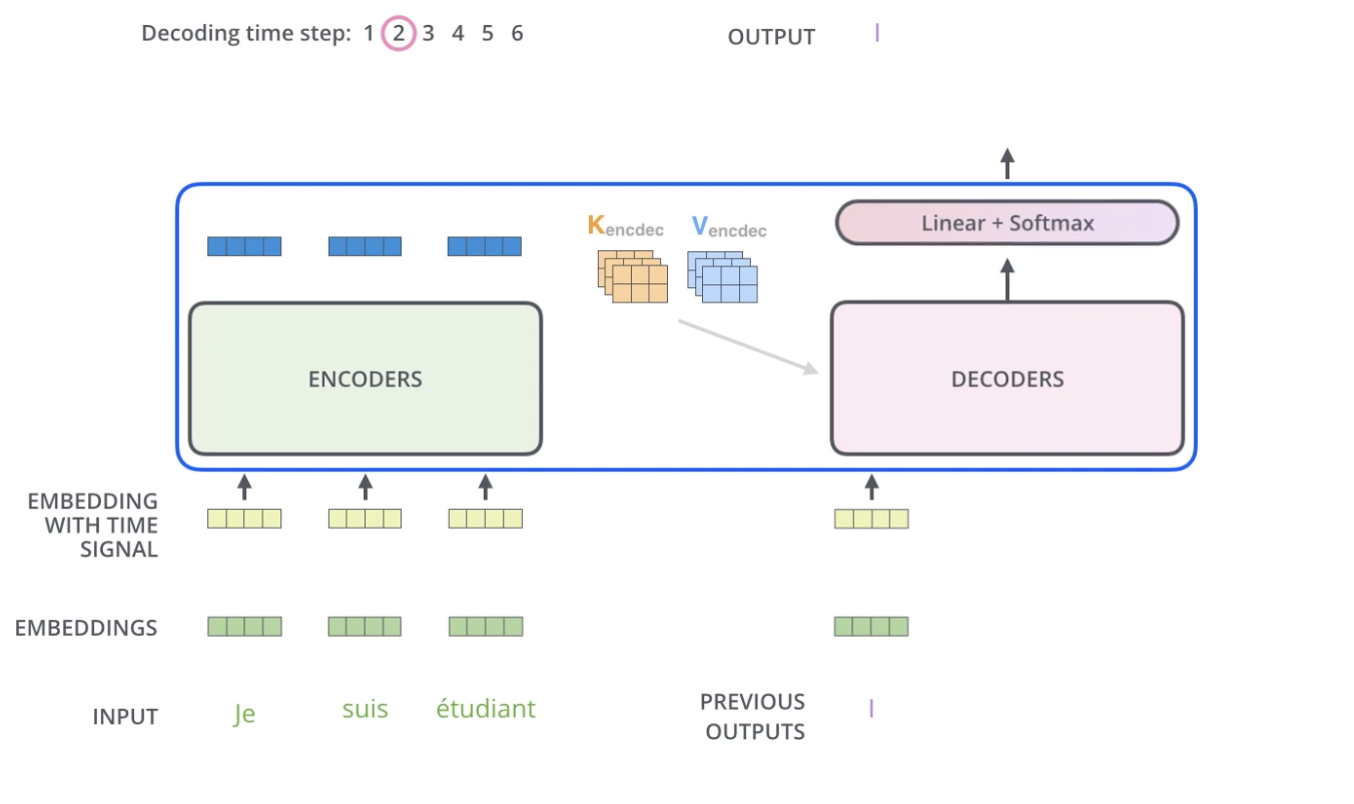
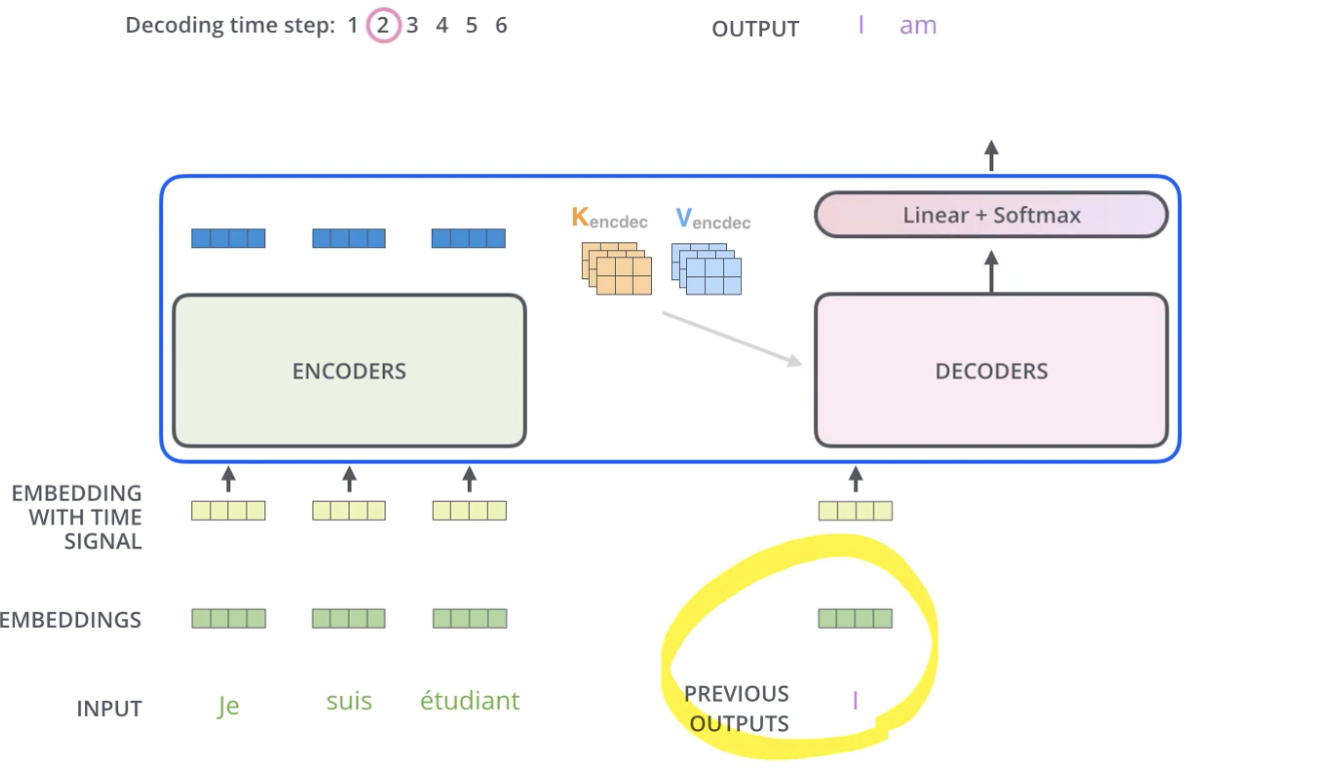
decoder에서는 masking이 돼 값들이 sequencial 하게 들어가고, encoder의 k, v가 지속적으로 decoder의 attention score 값에 영향을 끼친다.
총 3가지의 attention이 있는데,
- encoder 내부 self attention
- decoder 내부 masked self attention
- encoder의 output과 decoder과의 attention
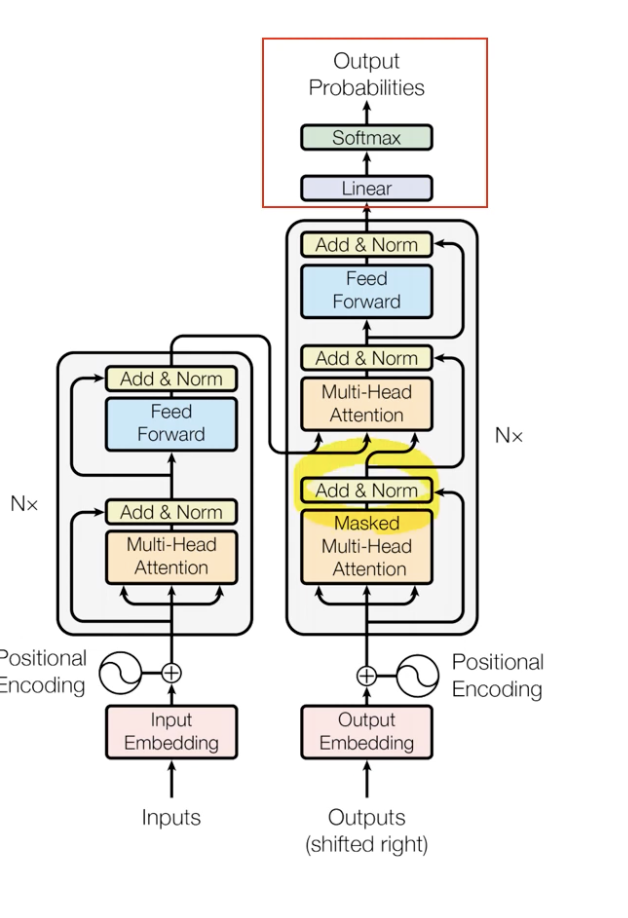
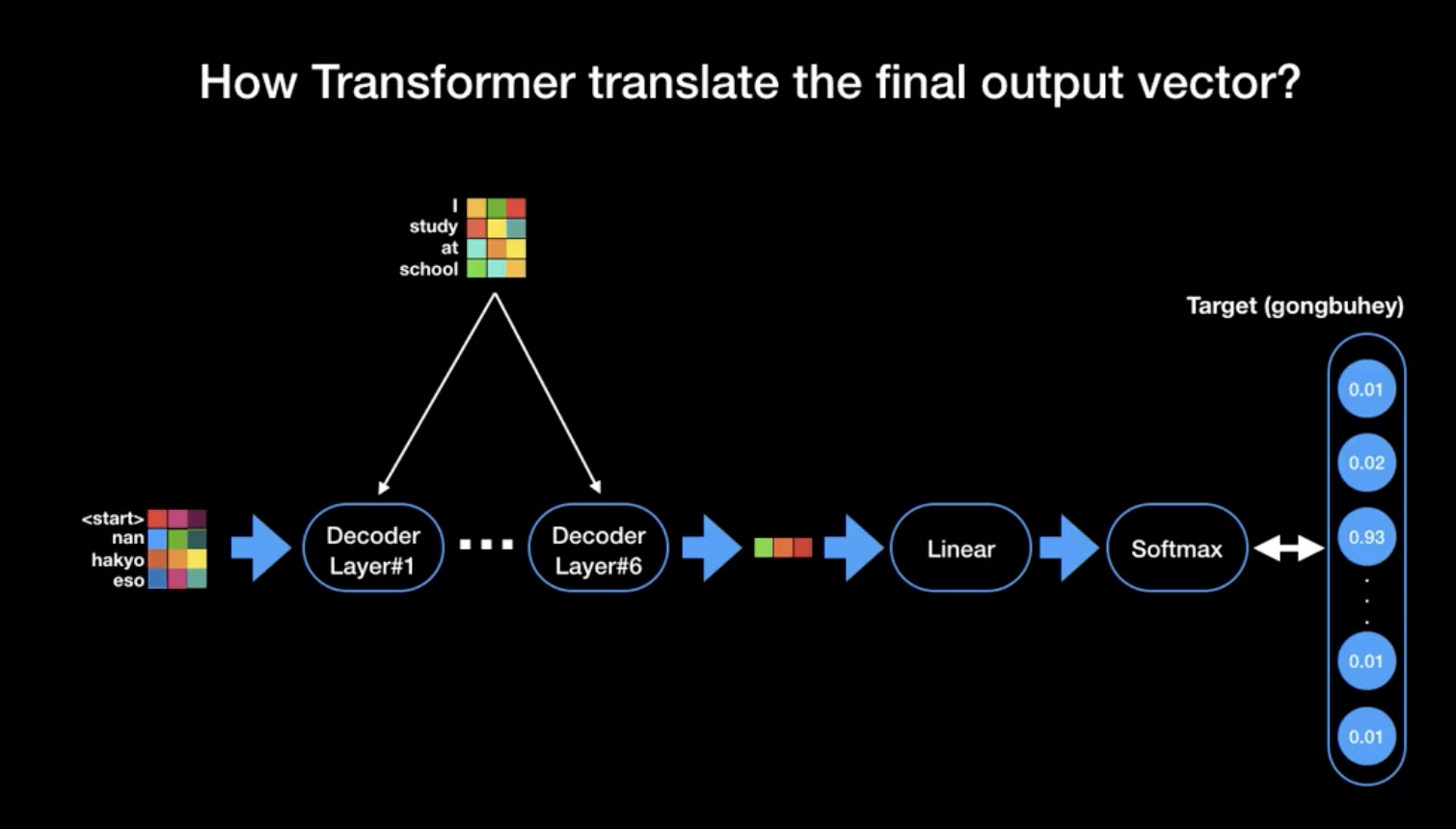
이제 마지막의 Final Linear와 Softmax Layer를 살펴보자
- Linear layer : a simple fully connected neural network that projects the vector produced by the stack of decoders into a much larger vector called a logits vector
- Softmax layer : turns those scores into probability
최종적으로 우리가 찾아야하는 단어가 무엇인지를 보여주는 과정이다.
*Reference*
Jay alamma - The Illustrated GPT-2 (Visualizing Transformer Language Models)