[CS231n review] Lecture4 - Backpropagation and Neural Networks
Stanford CS231n(2017)를 학습하며 정리 및 추가한 내용입니다.
Backpropagation and Neural Networks
거대한 모듈에서 한꺼번에 계산하는 것은 불가능하다.
FP : Forward Pass
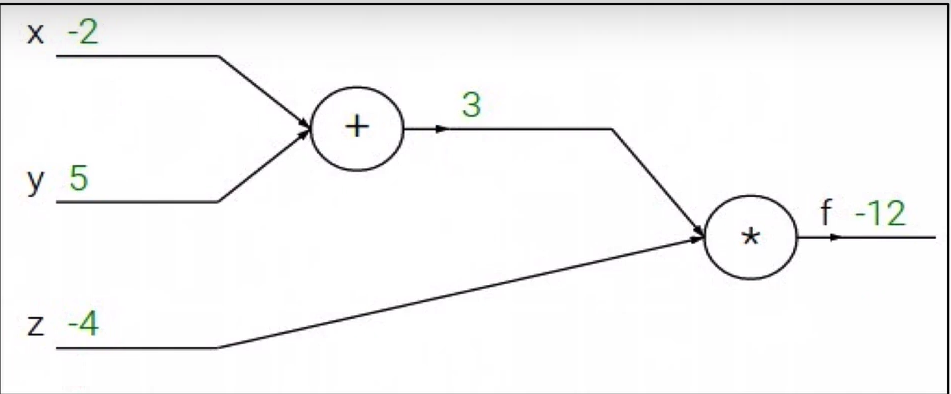
$f(x,y,z) = (x+y)z$
$x = -2, y=5, z=-4$
$q = x + y$ , $\frac{\partial q}{\partial x}=1$, $\frac{\partial q}{\partial y} = 1$
$f = qz$, $\frac{\partial f}{\partial q} = z$, $\frac{\partial f}{\partial z} = q$
원하는 것 : $\frac{\partial f}{\partial x}$, $\frac{\partial f}{\partial y}$, $\frac{\partial f}{\partial z}$
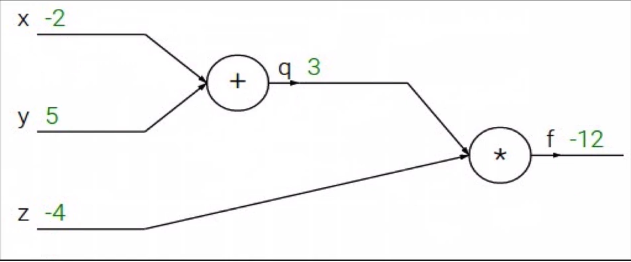
위 $\frac{\partial f}{\partial x}$, $\frac{\partial f}{\partial y}$, $\frac{\partial f}{\partial z}$ 를 구하기 위해서는 BP(Backward Pass, Backpropagation)을 해야한다.
$\frac{\partial f}{\partial f} =1$
$\frac{\partial f}{\partial z} =3$
$\frac{\partial f}{\partial q}=-4$
$\frac{\partial f}{\partial z}=3$
$\frac{\partial f}{\partial y} =-4$ , Chain rule :$\frac{\partial f}{\partial y} = \frac{\partial f}{\partial q} \frac{\partial q}{\partial y}$
forward pass 하는 과정에서 “local gradient”를 구할 수 있다.
local gradient 를 미리 구하여 저장한 후 chain rule을 이용하여
$gradient = local \ gradient \times global\ gradient$를 구한다.
- 아무리 깊고 복잡하여도 chain rule을 이용하여 gradient를 구할 수 있다.
- forward pass를 통해 Local gradient를 미리 저장한다.
sigmoid function : $\sigma (x) = \frac{1}{1+e^{-x}}$
sigmoid function을 미분하면 $(1-\sigma(x))\sigma(x)$으로 나타난다.
따라서 비슷한 형식인 $f(w,x) = \frac{1}{1+e^{-(w_{0}x_{0} + w_{1}x_{1}+w2)}}$의 미분또한 위의 형식으로 간단하게 구할 수 있다.
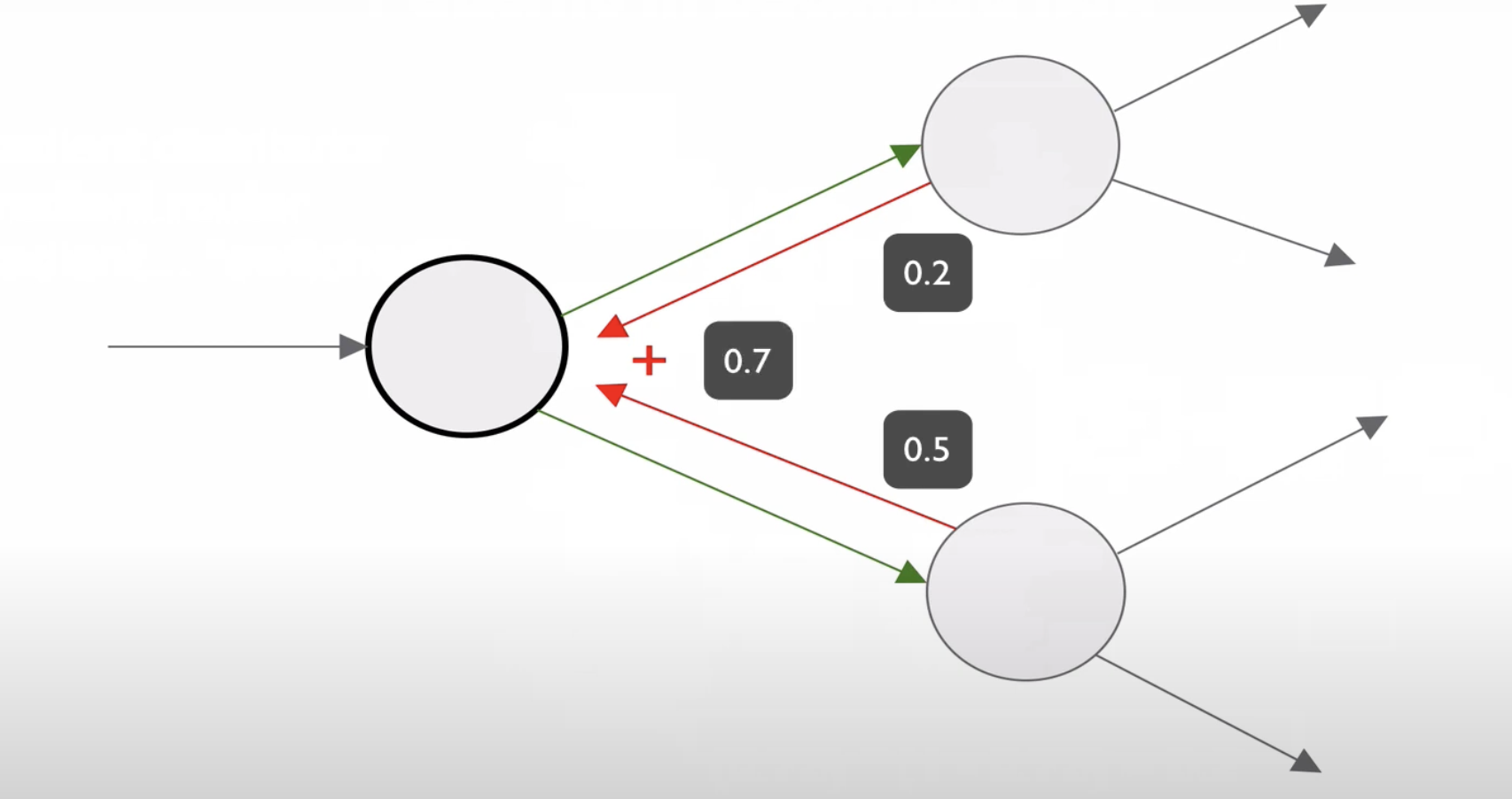
위와 같이 뒤가 여러 개로 나눠져있을 때 뒤의 gradient를 더해서 구할 수 있다.
Patterns in backward flow
gradient를 계산하는 backward 과정에 패턴이 있습니다.
add, max, mul gate
- add gate : gradient distributor
- 전의 gradient를 그대로 전파. local gradient의 값이 1이라서
- 두 개의 브랜치와 연결되는 덧셈 게이트는 upstream gradient를 연결된 브랜치에 같은 값으로 나눠줌
- 1로 나누면 그대로의 값이 나옴
- max gate: gradient router
- 여러 개 중에 하나만 취해주기 때문에
- mul gate: gradient… ‘switcher?’
- local gradient가 바뀌기 때문에
local gradient
local gradient는 forward pass 때 구할 수 있다.- local gradient forward pass 때 구해서 메모리에 저장해둔다.
global gradient
- backward pass 동안에만 구할 수 있다.
- 즉, local gradient랑 global gradient를 곱해서 gradient를 구할 수 있다.
- backward pass 때 chain rule이 일어난다.
Neural Network
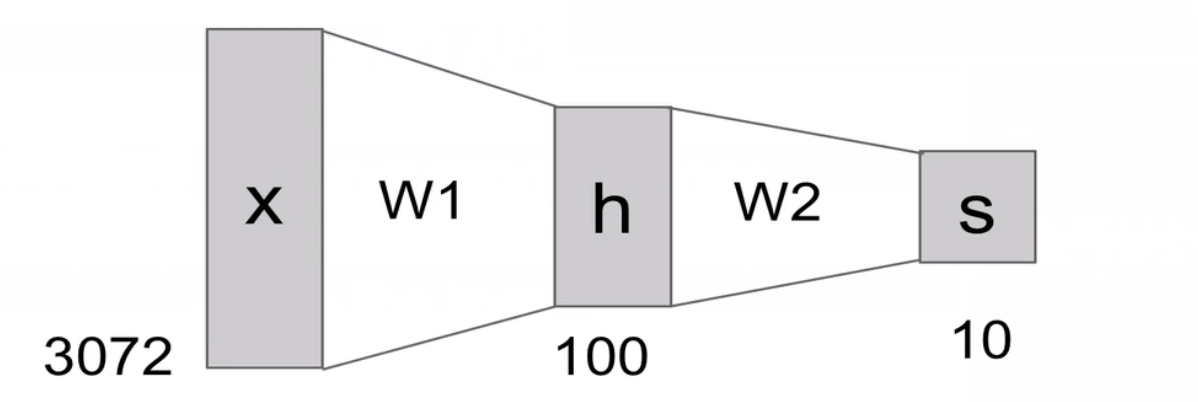
2-layer Neural Network : $f = W_{2}max(0,W_{1}x)$
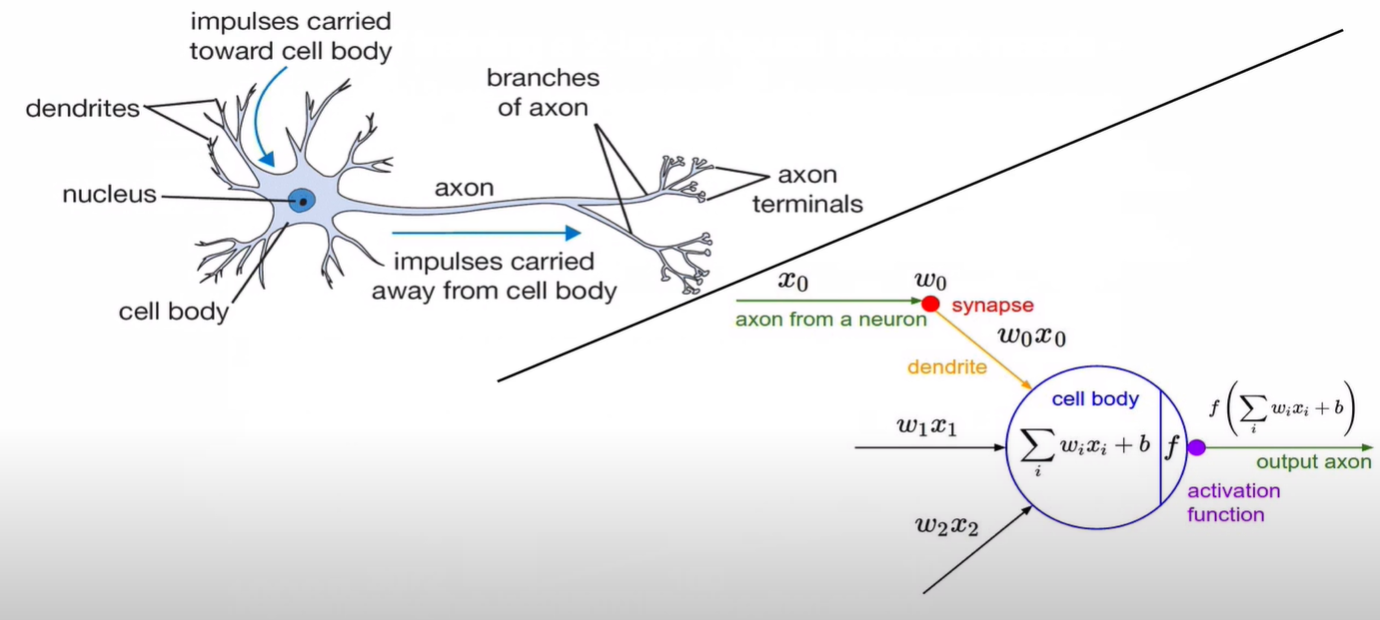
Activation Function

가장 많이 사용하는 Activation function은 ReLU
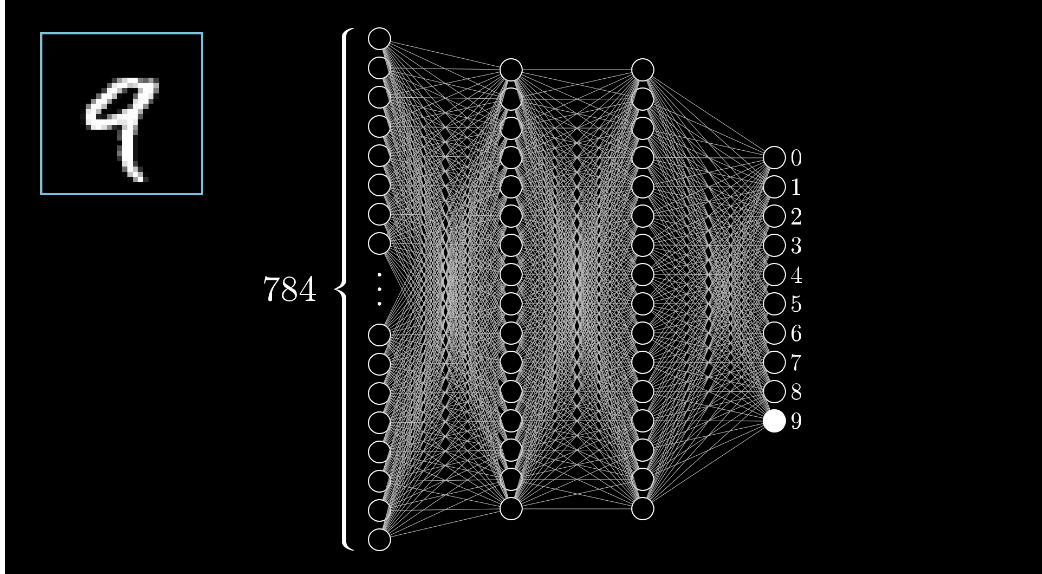
Neural networks: Architectures
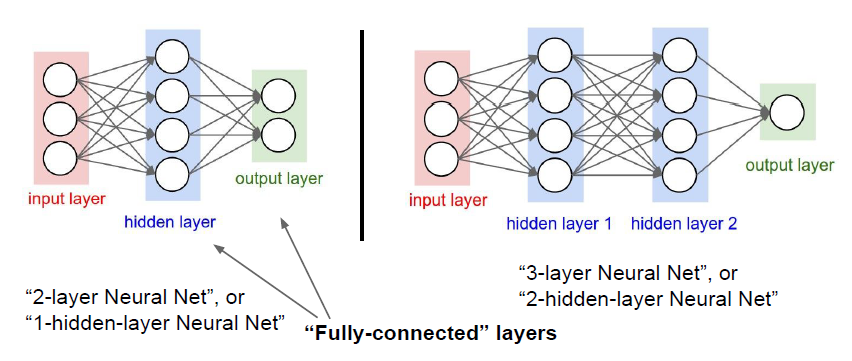
layer가 3개인데 2-layer라고하는 이유는, weight가 있는 것만 layer라고한다.
input layer는 weight가 없기때문에 제외돼 2-layer라고 부른다.
FC(Fully connected) layers : 모든 노드들이 연결되어있는 layers
layer로 구성하는 이유는 효율적으로 계산을 할 수 있기 때문