[CS231n review] Lecture3 - Loss function & Optimization
Stanford CS231n(2017)를 학습하며 정리 및 추가한 내용입니다.
Loss function & Optimization

Lecture 2에서 배운 바와 같이, 학습한다는 것은 좋은 $ W(parameter) $ 를 찾는 것이다.
해당 강의에서는 좋은 W를 찾는 과정에 대해 학습했다.
Loss function
좋은 W를 찾기 전에 가장 먼저 정해야 할 것이 있다.
무엇이 좋은 것인가?
무엇이 좋은 W인지 판단하기 위해 $Loss function$을 정해야한다.
loss function은 cost function, objective라고도 불린다.
강의에서, Loss function을 기준으로 SVM classifier와 softmax classifier를 설명한다.
1. SVM Classifier
$ x_{i}$ 는 이미지이고, $y_{i}$ 는 정답 라벨링일때, $s =f(x_{i},W)$를 통해 s를 구한다.
SVM은 Hinge Loss라고도 불리며 아래와 같이 구성된다.
\[L_{i} = \begin{cases} 0 & \text{if} \ s_{y_{i}} \ge s_{j} + 1, \\ s_{j}-s_{y_{i}} + 1 & \text{otherwise} \end{cases}\]SVM loss는 $ L_i = \sum_{j \ne y_i} max(0, s_j - s_{y_{i}} + 1)$ 와 같은 형태를 가진다.
여기서 $s_j$ 는 잘못된 label 의 score, $s_{y}_{i}$는 제대로 된 label의 score이고, $1$은 safety margin이다.
전체 training Loss 평균은 $L = \frac{1}{N} \sum_{i = 1}^N L_{i}$로 표현할 수 있다.
Q. What happens to loss if correct scores change a bit?
A. Nothing , correct score to be greather than one more than incorrect score.
Q. What is the min/max possible loss?
A. min : 0, Max : infinitely
Q. At initialization W is small so all $s \approx 0$. What is the loss
A. number of Class - 1
W가 매우 작아지면 정답 라벨을 제외한 모든 score은 $0-0+1$로 구해지기때문에, 결국 정답라벨을 제외한 Number of Class - 1에 1을 곱한 값이 loss가 된다.
Q .What if the sum was over all classes? (Including $j = y_i$)
A. loss increase by one
정답 라벨의 score은 $0-0+1=1$이기때문에 정답라벨을 포함한(모든 class)의 loss sum은 이전보다 1 증가한다.
Q. What if we used $L_i = \sum_{j \ne y_i} (0, s_j - s_{y_{i}} + 1)^2$?
A. 위는 non-linear way로 different loss fnction이다.
$f(x,W) = Wx$
만약 $L = 0$을 만족시키는 W를 찾았을 때, W는 유일한가?
-
Problem : 2W 또한 $L=0$을 만족한다.
--> 어떤 W가 좋은 W인가? 에 대한 문제가 발생한다.
이는 train loss에만 신경을 쓰고 있기 때문이고, 오직 train data 에만 신경을 쓰는 $W$를 선택하게 된다면 오버피팅의 문제가 발생한다
-
Solution : Weight Regularization
$\lambda$ 는 regularization strength로 하이퍼파라미터의 일종이다.
$\lambda R(W)$는 regularization loss이며, 이는 train data에 대한 성능을 낮추지만 test data(처음 보는 데이터)의 성능을 높일 수 있다.
Common use
- L2 Regularization
- L2 Regularization을 Weight Decay라고도 한다.
- L2 Regularization은 행렬 $W$에 대한 Euclidean Norm이다.
- $L_2 norm$을 사용하면 $L_2$정규화라 하며 이를 Ridge regression이라고 한다.
- L1 Regularization
- Elastic net(L1 + L2)
- Max norm regularization
- Dropout
Softmax Classifer
Softmax 는 Multinomial logistic regression이다.
softmax function 은 score를 전부 이용하고, 이 score에 지수를 취해서 양수를 만든다.
logistic Regression에 대하여
선형 회귀분석과는 다르게 종속 변수가 범주형 데이터를 대상으로 하며 입력 데이터가 주어졌을 때 해당 데이터의 결과가 특정 분류로 나뉘기 때문에 분류 기법으로 볼 수 있다.
-
두개 이상의 범주를 가지는 문제가 대상인 경우에 multinomial logistic regression이라고 한다.
The goal of binary logistic regression is to train a classifier that can make a binary decision about the class of a new input observation
-
The sigmoid function
로지스틱 모형 식은 독립변수가 어느 숫자이든 상관없이 종속변수 가 항상 범위 [0,1] 사이에 있도록 한다.
이때 odds를 logit 변환을 수행함으로써 얻어진다. (이에 대한 자세한 설명)
softmax 함수를 거치게 되면 확률 분포를 얻을 수 있고, 해당 클래스일 확률로 표현된다.
\[P(Y=k|X=x_{i})=\frac{e^s k}{\sum_{j}e^sj}\]scroes = unnormalized log probabilities of the classes
다시 말해, softmax는 입력 값을 출력으로 0~1 사이의 값으로 모두 정규화하며 출력 값들의 총합은 항상 1이 되는 특성을 가지는 함수이다.
분류하고 싶은 클래스의 수만큼 출력으로 구성하며 가장 큰 출력 값을 부여받은 클래스가 확률이 가장 높은 것으로 이용된다. \(L_i=-logP(Y=y_i|X=x_i)\)
\(L_i = -logP(Y=y_i | X = x_i)\) 이고, 이는 \(L_i=-log\frac{e^sy_i}{\sum_je^sj}\) 이다.
Q. What is the min / max possible loss $L_i$?
A. Min: 0 , Max : infinitely
Q. Usually at initialization W is small so all $s \approx 0$. What is the loss?
A. unnormalized log probabilities : 0
unnormalized probabilities : 1
Probabilities : $log\frac{1}{num\ of\ C}$ ($ = log C$)
SVM VS Softmax
무엇이 다른가?
관점의 차이가 있는데, SVM은 class score의 수치 자체보다는 정답 score과의 차이(margin)에 초점을 맞추었고, Softmax는 확률을 구하여 -log 에 초점을 맞추었다.
SVM loss는 정답 score을 미세하게 조정하여도 변하지 않지만, softmax는 변한다.
그 이유는 softmax는 정답 score가 충분히 높고, 다른 오답 score가 낮은 상황에도 정답 score를 높이는데 (1로) 초점을 맞추기 때문이다.
Optimization
Optimization은 왜 하는건가? 에 대한 답은 한마디로 “Minimize Loss”이다.
이 optimization에서는 여러 strategy가 존재한다.
그 중 첫 번째로 $very \ bad \ idea \ solution$라고 소개한 Random search를 소개한다.
- Random search
Random search 는 말 그대로, 정말 random하게 찍어서 좋은 결과가 나온 값을 갱신하는 방식이다. 강의에서 소개한 바에 따르면 그냥 찍어도 10%의 정확도가 나오는 환경에서 Random search 후 15.5%가 나오는 매우 낮은 정확도를 보인다.(강의자료에는 “not bad”라고 명시돼 있다. 어떤 정리 영상에서 이가 나쁘지않은 결과라고 “not bad”라고 설명하는 영상이 있었는데, 이는 조롱의 의미이다.)
- Follow the slope
이는 parameter 공간에서 gradient를 이용하여 gradient 가 가장 가파른 곳을 찾아 최선의 방향으로 이동하는 것을 말한다.
이때 미분이 상당히 중요하게 역할하는데, 그 이유는 gradient는 미분으로 구할 수 있기 때문이다.
이때, gradient 계산 방법은 2가지로 나뉜다.
- Numerical gradient
$h$라는 작은 변화를 통해 loss function을 통해 변해진 loss 값을 보고, 계산하는 것으로 0.0001의 작은 값이면 충분하다고 한다.
그러나 gradient를 계산하는데 드는 비용은 parameter 수에 따라 선형적으로 증가하며, 데이터가 커질 수록 이 문제는 심각해지는 치명적인 문제가 존재한다.
- Analytic gradient
근사치가 아닌 정확한 수식을 이용하기 때문에 계산하기 매우 빠른 장점이 존재하지만, error가 발생할 가능성이 있는 문제점이 있다.
따라서 analytic gradient를 이용하면서, numerical gradient를 통해 검증하는 과정을 거친다.(이를 gradient check라고 한다.)
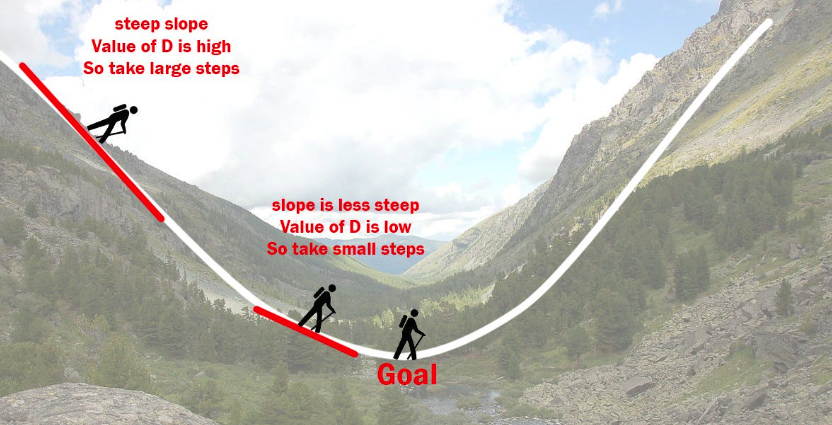
이 강의에서는 “산에 있는 것을 상상해보자”라고 한다. 우리가 산의 어디에 있는지 몰라도 경사가 어느 방향인지 알 수 있다.
그렇게 조금씩 산에서 경사를 따라 내려오는 것이 경사하강법의 직관적 이해이다.
-
Gradient Descent
Gradient Descent는 경사하강법이라고 불리는데, 우선 $W$를 임의의 값으로 초기화한다.
그리고 loss와 gradient를 계산한다.
while True: weight_grad = evaluate_gradient(loss_fun, data, weight) weight += - step_size * weights_grad # perform parameter update이때 gradient가 loss를 가장 빠르게 높이는 방향을 알려주기 때문에 $-$ 를 취해 loss를 가장 빠르게 작아지는 방향을 찾아,
step_size만큼 이동한다.이를 반복하면 결국 수렴하게 된다.
step_size는 hyper parameter이고, 이는 gradient 방향으로 얼마나 나아가는지를 설정한다. 이를learning rate라고도 하고(줄여서lr),alpha라고도 한다.-
Problem
gradient를 한 번 계산할 때마다 전체 training data set의 전체 N개를 한번 더 위와 동일한 방식으로 돌아야하는 비효율 적인 문제가 발생한다.
이를 해결하기 위한 방법이 Stochastic Gradient Descent (SGD)이다.
-
-
Stochastic Gradient Descent (SGD)
Stochastic Gradient Descent (SGD)는 쉽게 말해, 표본 추출이다.
while True:
data_batch = sample_training_data(data, 256)
weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
weights += -step_size * weights_grad
Minibatch는 training data를 작은 sample 집합으로 나눠 학습하는 것이다.
(이때 관례적으로 2의 제곱값인 32개, 64개, 128개, 256개를 주로 이용한다.)
